해당 차시 학습지 파일
학습 목표
- 물질파 이론을 근거로 입자의 파동성을 설명할 수 있다.
- 전자 회절 실험을 통해 입자의 파동성을 증명할 수 있다.
우리는 꿈을 이루어 가는 과정에서 강한 자존심과 욕망을 느끼면서도 동시에 겸손과 정의로 무장하는, 다소 양가적인 감정을 갖게 됩니다. 그러나 이 두 감정이 정말 다르기만 할까요? 서로 모순된 듯 보이는 두 감정이 사실은 서로를 비추며 하나의 본질을 이루어 가는 것이라는 삶의 철학과 같은 결을 공유하는 물리학을 배우는 시간입니다.
물리학의 흐름
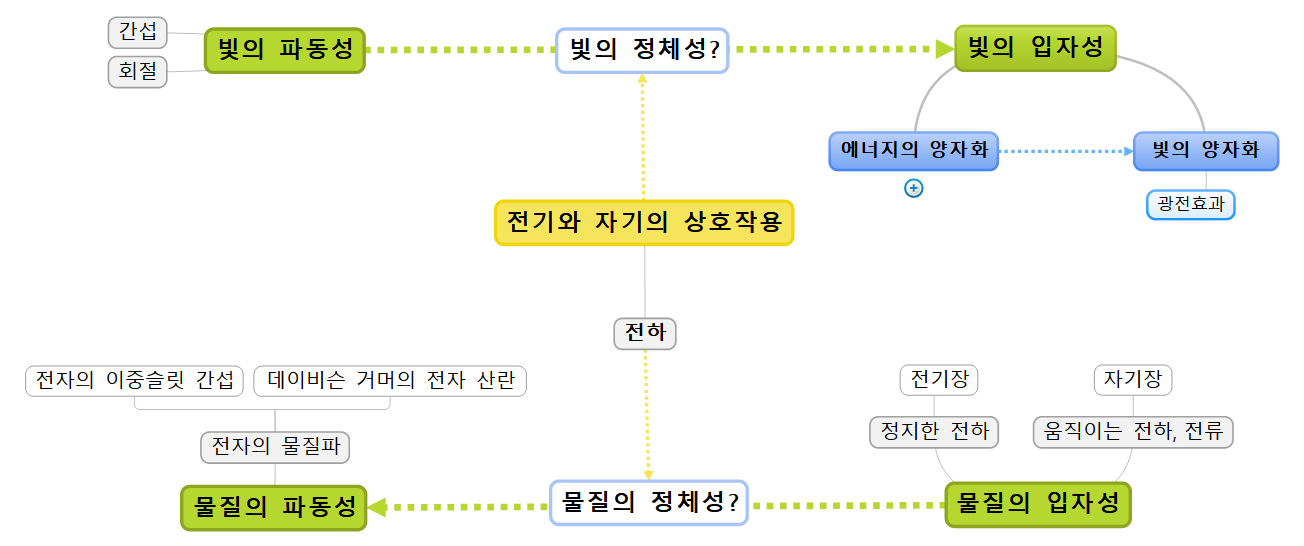
다른 것들에 등가성의 다리를 놓다.
1905년에 아인슈타인이 마지막으로 출판한 네 번째 논문에는 유명한 식이 등장합니다.
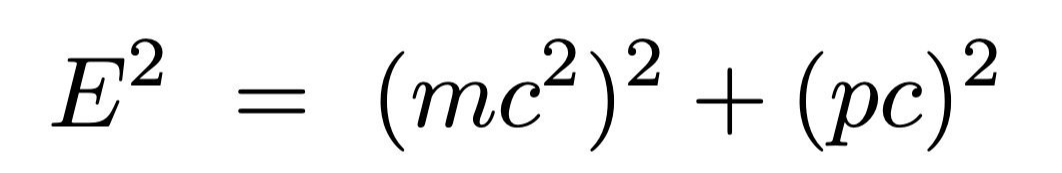
문제는 질량이 0인 빛이에요. 식의 첫 번째 항이 0이 되고, 뉴턴역학에서의 운동량 p은 움직이는 물체의 질량 m과 속도 v의 곱으로 정의되기에 두 번째 항도 0이 됩니다. 따라서 빛의 에너지 E는 0이 돼요. 그러나 빛은 c라는 속력으로 끊임없이 움직이는 에너지 덩어리임이 자명합니다. 따라서 에너지와 운동량이란 속성은 여전히 남아있습니다. 이러한 모순은 질량 에너지 등가 원리로 해결할 수 있는데요. 이에 따르면 질량은 더 이상 물질적인 것에 불과하지 않은 에너지의 한 형태이며 질량과 에너지는 서로 전환될 수 있습니다. 다시 말해 빛은 질량이 없어도 c라는 속력으로 끊임없이 움직이는 에너지 덩어리이며 그 에너지의 크기 E는 pc입니다. 그렇다면 빛의 운동량 p는 어떻게 정의해야 할까요?
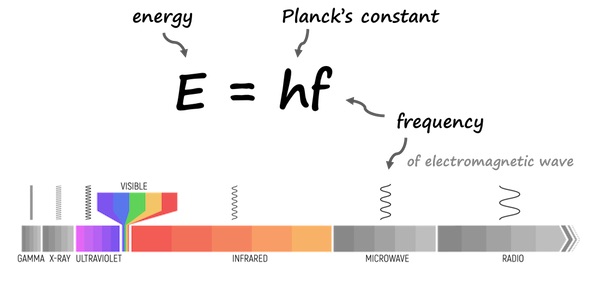
다른 한편으로 광양자론은 빛 알갱이가 갖고 있는 에너지를 E=hf으로 표시해 주었습니다. 그렇다면 빛의 에너지를 표현하는 데는 두 가지 방식이 존재한다는 결론에 도달합니다.
E = pc와 E = hf
만약 두 식이 동일한 빛 알갱이의 속성을 표현하는 서로 다른 방식에 불과하다면 어떤 일이 생길까요? 당연히 두 식은 동등해야 합니다. 여기서 마침 양변에 공통으로 등장하는 빛의 속력 c를 소거하고 나면 p=h/λ라는 관계가 남습니다.
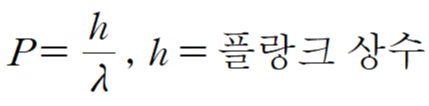
가만히 생각해 보면 이 식의 의미가 조금 알쏭달쏭합니다. 운동량은 뉴턴역학 이후로 줄곧 입자의 전형적인 속성으로 알려져 있었어요. 반면 파장은 파동의 전형적인 속성이었고요. 빛 알갱이에는 이 두 가지 속성이 공존합니다. 파동인 줄 알았던 빛에는 입자의 속성, 즉 운동량도 있습니다. 그 두 속성은 플랑크 상수를 통해 서로 연결된, 사실은 동일한 입자의 속성을 표현하는 서로 다른 언어일 뿐이었죠. 빛의 파장값을 토대로 빛의 운동량을 알 수 있게 됐습니다. 그렇다면 반대로 어떤 운동량을 갖는 입자에는 그에 해당하는 파장이란 파동적 속성이 있지 않을까란 생각을 할 수 있지 않았을까요? 그 장본인이 바로 드브로이입니다.
1. 물질파

드브로이는 자연의 대칭성에 입각하여 다음과 같은 주장을 합니다. "전하가 만들어낸 빛이 이중성을 전제한다면, 그의 모체인 전하 역시 입자이기도 하면서 파동이지 않을까?" 이에 드브로이는 전자를 비롯한 입자들 역시 에너지와 운동량을 파동의 형태로 전달할 수 있음에 착안하여 입자의 파동적 성질, 물질파를 정의합니다.

드브로이 관계식은 입자의 운동량 P와 입자의 물질파 파장 λ의 대응 관계를 가정한 것입니다. 오해하지 마세요. 물질이 파동처럼 넘실넘실거린다기보다는 파장 λ만큼의 파동적 성질(=굴절 및 간섭)을 보여주겠거니 생각해야 합니다.
운동에너지로 표현하는 드브로이 관계식

2. 입자의 파동성이 관찰되다.
1) 전자의 회절

물질파의 존재에 대한 드브로이의 예측은 3년 후 실험으로 검증됩니다. 전자와 양성자, 중성자 심지어 전자보다 50만 배나 무겁고 복잡한 요오드 분자를 이용한 실험에서도 입자들이 파동만이 갖는 특성인 회절 무늬를 보였거든요.
2) 이중 슬릿에서 전자의 간섭 무늬
음극선은 전자의 흐름입니다. 정지해 있던 바람개비가 돌아가는 이유는 전자가 바람개비와 충돌하여 운동량을 전달하기 때문이죠. 이 현상은 전자가 질량을 가진 입자임을 입증합니다.
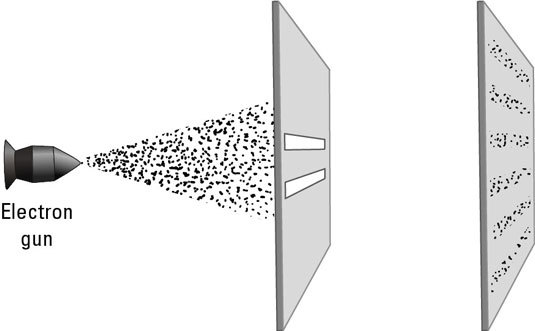


그러나 전자가 마냥 입자이기만 했다면 이중 슬릿을 통과한 전자는 스크린 상에 두 군데에만 도달했을 거예요. 하지만 실험 결과, 전자의 양이 많은 지점과 적은 지점이 번갈아 나타나는 소위 간섭무늬가 스크린에 나타납니다. 이는 전자가 파동처럼 행동했다고 봐야 설명이 되죠. 즉 전자는 파동적인 성질을 갖습니다.
간섭 무늬 간의 간격
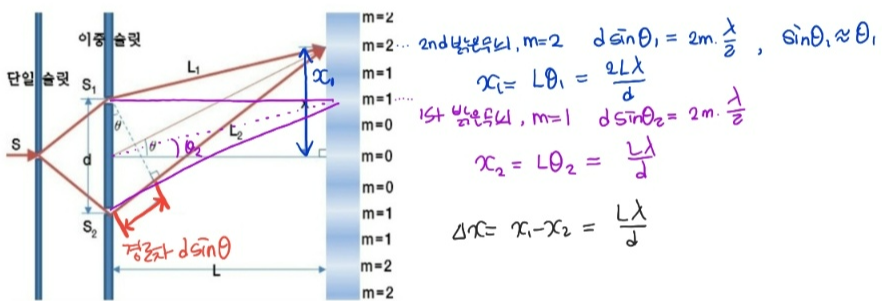
드브로이 관계식으로 정의한 λ값을 이용해 예측한 전자 간섭 무늬 간의 간격(△x)은 소름 돋을 정도로 실제 관측값과 똑같습니다. 이를 통해 드브로이의 물질파 이론은 힘을 얻게 되었어요.
3) 데이비슨-거머의 전자 산란 실험
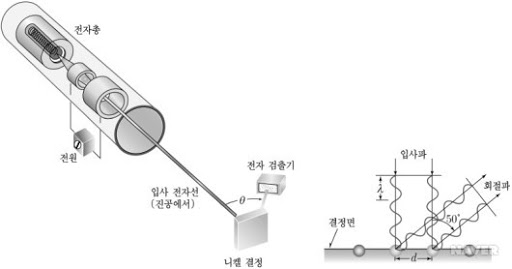
데이비슨과 거머는 가속된 전자들을 니켈 결정의 한 면에 입사시켰을 때 튀어나오는 각도에 따른 전자들의 분포를 관측하였어요. 그들은 전자의 파동성에 입각하여 전자가 특정 각도에서 보강 간섭을 일으켜 강하게 산란할 것이라는 예측을 했고, 실제로 특정 각도에서 산란이 강하게 일어남을 확인합니다.
브래그 회절 조건

'브래그 회절 조건'은 특정 각도로 입사한 전자가 강한 회절 무늬를 나타내는 조건입니다. 니켈 결정의 d는 X선의 간섭을 이용해 0.91옴스트롱임을 밝혀냈어요. 전자가 입사한 특정 각도를 브래그 조건에 대입하면 n=1인 경우에 전자의 물질파 파장은 1.65옴스트롱이 나옵니다. 한편 전자의 가속 전압이 54V이므로 입사하는 전자는 54eV의 에너지를 가집니다. 이 값을 드브로이 물질파 식에 대입하면 파장값은 1.67옴스트롱이에요. 이는 드브로이 물질파 이론이 예측한 값과 실재가 거의 일치함을 의미합니다.
물질의 이중성
빛이 이중적이듯 물질 또한 이중적이라서 물질 역시 어떤 때에 파동처럼 어떤 때에 입자처럼 행동합니다. 우리의 거시 세계에서는 물질의 파동성을 관찰하기 어렵죠. 그 이유는 드브로이 관계식으로 설명할 수 있습니다.


플랑크 상수 h가 워낙에 작다 보니 분모의 질량이 너무 커져버리면 물질파 파장이 0으로 수렴하여 물질의 파동성을 논하는 게 의미 없어집니다. 다시 말해 전자는 일종의 물질파이며 자기 자신과 간섭을 하지만 우리는 물질파가 아니며 자기 자신과 간섭을 할 수가 없습니다.
가능성의 확률을 입체적으로 따지는 양자 역학
E=pc와 E=hf, 서로 다른 식 사이에 등가성의 다리가 놓이면서 입자성과 파동성을 단적으로 보지 않고 입체적으로 파악하기 시작했습니다. 이로 인해 미시 입자의 확률적 거동을 설명하는 양자 역학이 태동하였어요. 양자 역학은 우리의 감각을 넘어서는 시공간에 대한 이해를 도와주기도 했지만 미시 세계의 실체에 대한 우리의 이해를 더욱 낯선 것, Alien thing으로 만들었습니다. 가능성의 확률과 의식을 지닌 존재의 관찰 행위를 입체적으로 판단하는 양자 역학은 뭐든 단정 짓고 결정하는 뉴턴의 고전 역학에서 벗어나지 못한 우리에게는 '비상식적'이지만, 그 덕분에 우리는 스마트폰으로 와이파이를 통해 인터넷도 하고 내비게이션으로 길도 찾아가는 '상식적인' 일을 하며 살아갑니다. 이처럼 양자 역학은 인간에게는 다소 Alien하지만 우주의 설계도와도 같아서 외계인, Alien들도 알 수 있는 진리입니다.
Alien - 이수현
https://www.youtube.com/watch?v=UrsMx7Q_9IE
우리의 삶도 마찬가지예요. 우리가 꿈을 이루어 가는 과정에서 갖는 양가적인 감정, 강한 자존심과 욕망 그리고 겸손과 정의 사이에 등가성의 다리를 놓는다면 우리는 스스로를 입체적으로 파악할 수 있습니다. 강한 자존심과 욕망으로 화려하게 빛나는 내 모습도 겸손과 정의에 의해 윤곽이 또렷한 내 모습도, 서로 모순된 듯 보이는 두 모습 모두 하나의 나를 이루는 일부입니다.
가끔은 나 자신이 낯설고, 마치 이방인(Alien)처럼 느껴질 때가 있는데요. 그것은 내 안에 다양한 모습이 공존하기 때문입니다. 입체적인 자아는 곧 불확실성을 전제로 한 존재입니다. 불확실성은 우리를 불안하게 하지만, 동시에 우리가 성장하고 있음을 보여주는 증거이기도 해요. 양자 역학은 서로 다른 성질의 공존, 불확실성 속의 잠재력, 그리고 그 가능성을 현실로 만들어 가는 힘은 다름 아닌 의식을 지닌 존재, 나 자신에게 있음을 전합니다. 이수현의 Alien을 들으며, 오늘도 물리를 통해 인생을 배웁니다.
'물리학II 클립' 카테고리의 다른 글
| 원자 모형과 불확정성 원리 (2) | 2022.09.28 |
|---|---|
| 양자 역학 탄생의 신호탄, 광전 효과 (0) | 2022.09.22 |
| 볼록 렌즈에 의한 상의 형성 (0) | 2022.09.20 |
| 도플러 효과 (2) | 2022.09.14 |
| 파동의 회절 (4) | 2022.08.25 |



