해당 차시 학습지 파일
학습 목표
뉴턴 운동 법칙을 이용하여 물체의 포물선 운동을 정량적으로 설명할 수 있다.

학창 시절 성적은 바닥인 데다 습관적으로 지각을 일삼는 말썽꾸러기 낙제생이었지만 당시 세계 1등 국가의 장관과 수상을 역임하고, 유년 시절에 겪었던 언어 장애와 무대 공포증을 극복하고 훗날 최고의 연설가로 평가받은 사람. 바로 영국의 윈스턴 처칠입니다. 이러한 삶의 반전을 야기한 처칠의 태도를 오늘 공부할 물리학을 통해 배웁니다.
1. 수평으로 던진 물체의 운동

수평 방향으로 던져진 공은 그림과 같이 포물선 궤적을 그리면서 운동합니다. 포물선 궤적을 그리는 까닭은 이 운동을 수평 방향과 수직 방향으로 나눠서 분석하면 알 수 있습니다.
1) 수평 방향의 운동

공은 수평 방향으로 속력이 일정한 등속 운동을 합니다. 수평 방향으로 물체가 등속 운동하는 이유는 무엇일까요? 답은 뉴턴 운동 제1법칙 '힘이 작용하지 않는 물체는 정지해 있거나 등속 운동을 한다'에 있습니다. 그래요. 물체에 수평 방향으로 작용하는 힘 F이 0이기 때문이죠.
2) 수직 방향의 운동

공은 수직 방향으로 속력이 점점 증가하는 운동을 합니다. 다시 말해 수직 방향으로는 속력이 변하는 가속도 운동을 한다는 것이고, 속력이 변한다는 건 물체에게 수직 방향으로 힘 F이 작용함을 뜻합니다. 그렇다면 물체에 수직 방향으로 작용하는 힘은 무엇일까요?
시간-수직 방향 속력 그래프
| 수평으로 던진 물체의 수직 속력 | 자유 낙하 운동하는 물체의 속력 |
 |
 |
물체의 수직 속력을 시간에 따라 나타낸 그래프는 중력에 의해 자유 낙하 운동하는 물체의 '시간-속력 그래프'와 똑같습니다. 눈치채셨나요? 물체에 수직 방향으로 작용하는 힘은 바로 중력입니다.
3) 자유 낙하 운동 vs 수평으로 던진 물체의 운동
같은 지점에서 한 물체는 수평으로 던지는 동시에 다른 물체는 자유 낙하시킬 때, 어떤 물체가 지면에 먼저 도달할까요? 혹자는 수평으로 던져진 물체가 처음 속력이 있는 것만큼 빨리 움직이기 때문에 더 빨리 도달한다고 말합니다. 혹자는 수평으로 던져진 물체가 더 긴 궤적을 움직이기 때문에 지면에 더 늦게 도달한다고 말합니다. 누구의 말이 맞을까요? 실험으로 확인해 봅시다.
두 물체는 동시에 도달합니다. 그 이유를 시간-속력 그래프로 알아봅시다.


자유 낙하 하는 물체와 수평으로 던진 물체는 운동하는 동안 일정한 크기의 중력이 작용하여 수직 방향의 속력 변화가 같습니다. 만약 자유 낙하하는 물체가 지면에 닿는 데 3초가 걸렸다면, 수평으로 던져진 물체 역시 같은 낙하 거리를 같은 속력 변화로 운동하기 때문에 지면에 닿는 데 3초가 걸립니다.
포물선 운동과 일-에너지 정리
이때 수평으로 던져진 물체가 바닥에 도달하기까지 수평 방향의 운동은 수직 방향의 운동에 아무런 개입을 하지 않습니다. 이 상황에서 수평 방향의 힘이 0인 데다가 설령 그 힘이 0이 아닐지라도, 물체에 작용하는 수평 방향의 힘과 물체의 수직 방향으로의 변위가 구조적으로 수직 관계를 이루기 때문에 물체에 수평 방향으로 작용하는 힘이 물체가 수직 방향으로 변위하는 동안 하는 일이 0이 됩니다.
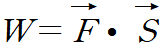

따라서 수평 방향의 운동은 수직 방향의 운동에 아무런 변화를 주지 못합니다.
2. 비스듬히 던진 물체의 운동
1) 정성적 분석
지면을 기준으로 비스듬히 던져 올린 물체는 포물선 궤적을 그리며 운동합니다. 이 물체에게 작용하는 알짜힘의 방향은 어디를 향할까요?
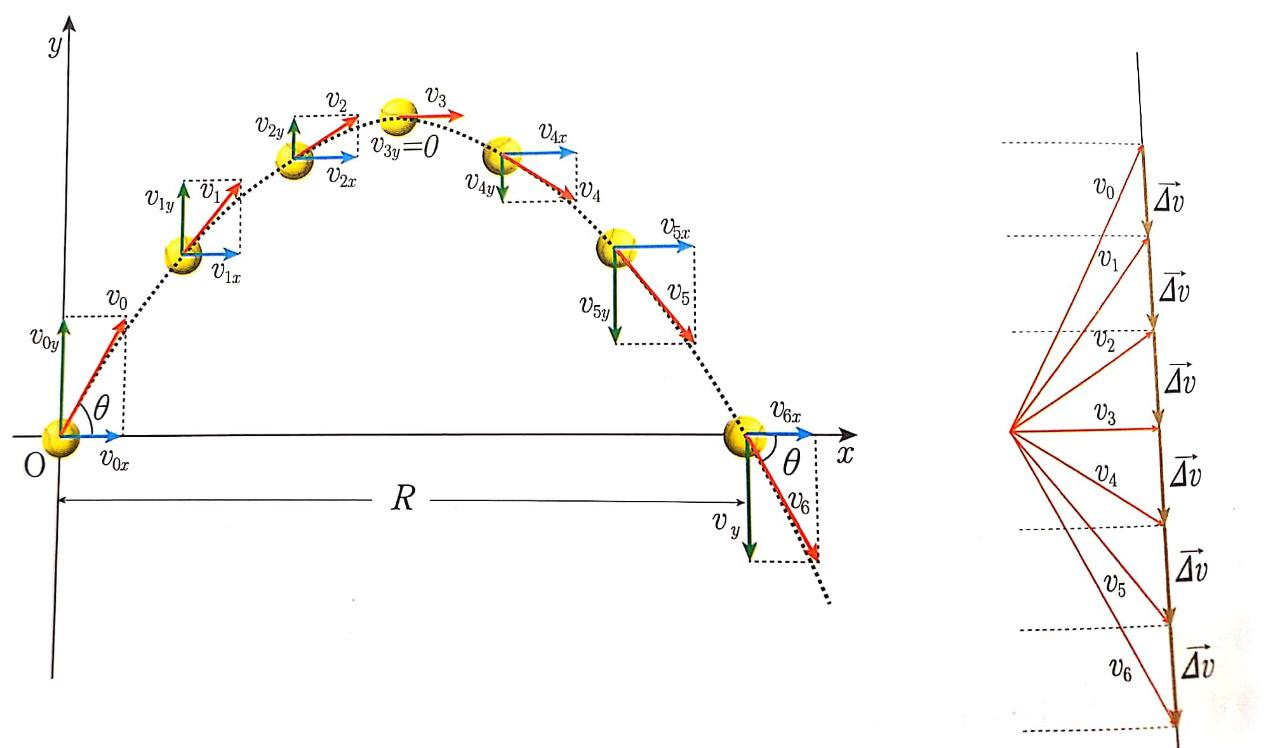
속도 벡터의 합성을 이용하면 가속도의 방향을 알 수 있습니다. 오른쪽 그림을 보면 가속도의 방향이 시종일관 아래를 향해요. 가속도의 방향은 곧 힘의 방향이기 때문에 이 물체에 작용하는 알짜힘의 방향은 아래입니다. 눈치챘겠지만 그 알짜힘은 중력이에요. 정리하면 포물선 운동하는 물체엔 중력 이외에 어떠한 힘도 작용하지 않기 때문에 수평 방향으로는 등속도 운동을 하고, 수직 방향으로는 등가속도 운동을 합니다.
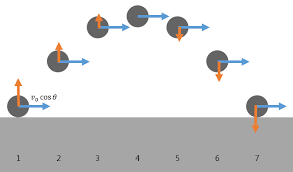
2) 정량적 분석
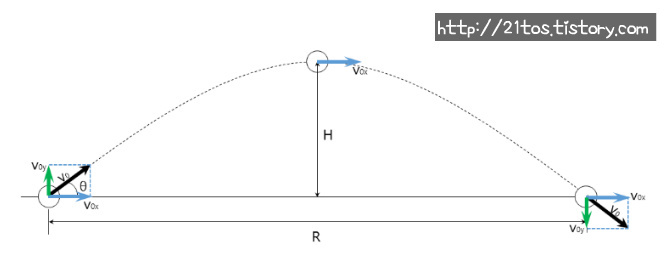
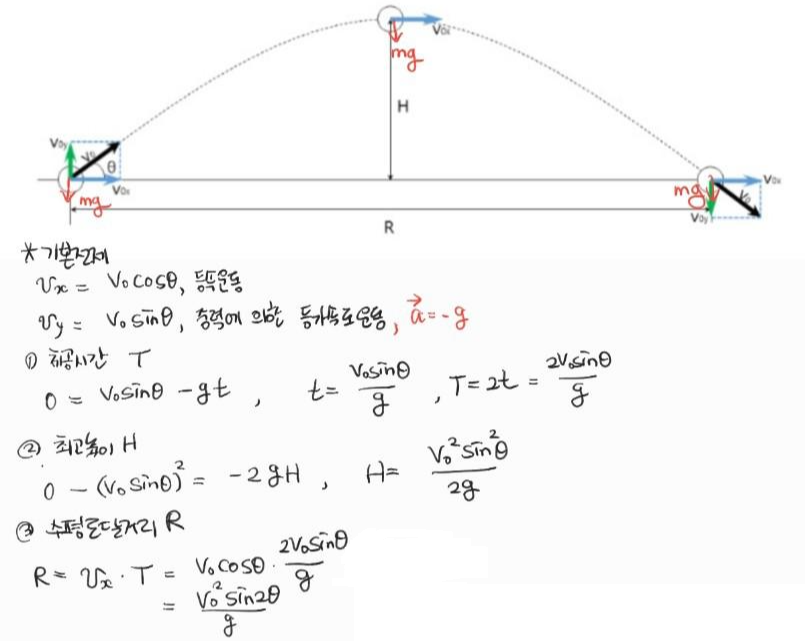
따라서 물체를 지표면으로부터 45˚의 각도로 던져 올릴 때 물체의 수평 도달 거리는 최대가 됩니다.
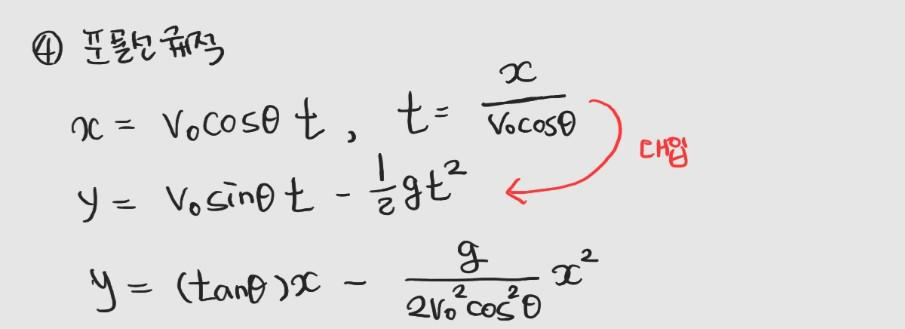
건물 사이에 피어난 장미 - H1KEY
https://youtu.be/Z_JNejGY0Hs?si=vmU2x1gLOkgwX0rt
"현재가 과거와 싸우면 미래를 잃는다"
과거에 얽매이지 않고 현재에 충실한 삶을 살아가며 절대로 포기하지 않았던 처칠. 그는 땅 위에서 피어나지 못한 현재를 원망하는 대신 어렵게 피어난 만큼 악착같이 살아내 보려는 건물 사이에 피어난 장미와도 같습니다. 모두가 자신의 향길 맡고 취해 웃을 때까지 삭막한 도시를 아름답게 물들였을 장미의 우직함은 처칠의 우직함과 같습니다. 이처럼 어떠한 상황이 닥쳐온들 중요한 건 꺾이지 않는 마음입니다.


하루하루 앞을 향해 나아가고 있지만, 마치 제자리걸음인 듯 느껴질 때가 있죠. 하지만 기억하세요. 우리의 인생은 '시간-속력 그래프'의 면적과 같다는 것을요. 당장 눈에 보이는 '시간-속력 그래프'의 추이는 정체되어 있지만 그 이면에 자리한 이동 거리는 계속해서 늘어나고 있습니다. 지금은 정체되어 있을지라도, 꺾이지 않는 마음으로 꾸준함을 유지한다면 그 꾸준함은 반드시 여러분의 역량을 늘릴 것입니다. 오늘도 물리를 통해 인생을 배웁니다.
'물리학II 클립' 카테고리의 다른 글
| 케플러의 법칙과 뉴턴의 만유인력 법칙 (0) | 2022.03.16 |
|---|---|
| 평면 상의 물체 운동 ② {등속 원운동} (1) | 2022.03.14 |
| 회전 운동과 물체의 무게 중심 (0) | 2022.02.28 |
| 힘의 합성과 알짜힘 (0) | 2022.02.28 |
| 물리학 II 수업 프리뷰 (0) | 2022.02.28 |




사이언스토리텔러님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.