해당 차시 학습지 파일
학습 목표
등속 원운동하는 물체에는 구심력이 작용함을 안다.
등속 원운동에서 구심력과 회전수, 회전 반지름 등의 관계를 설명할 수 있다.
째깍째깍, 무미건조하게 돌아가는 시곗바늘의 리듬에 맞춰 흘러가는 삶이 무료하게 느껴질 때가 있습니다. 남들의 시간은 앞으로 나아가는 것 같은데, 왜 내 시간은 쳇바퀴처럼 하릴없이 제자리만 도는 거 같은지. 분명 앞으로 나아간다고 생각했는데 막상 제자리였음을 알게 됐을 때 느껴지는 시간에 대한 배신감. 그 어설프고 초라한 시간의 째깍거림에 삐걱거리는 삶, 그 틈새에 스스로도 확신이 없는 불안이 쌓여갑니다. 우리는 그를 현타라 부르죠.
빙빙 돌아가는 시간을 따라 주기적으로 찾아오는 현타. 그에 휩쓸리지 않고 중심을 잡아가는 방법은 오늘 공부할 물리학이 가르쳐줍니다.
3. 등속 원운동
등속 원운동이란 물체가 원궤도를 따라 회전할 때 같은 시간 동안 같은 각도만큼 회전하는 운동을 일컫습니다. 즉, 등속 원운동은 단위 시간당 각도 변화량이 일정해요. 등속 원운동하는 물체의 속력은 일정하지만 방향은 원의 접선 방향으로 매 순간 변합니다.
1) 각속도와 선속도
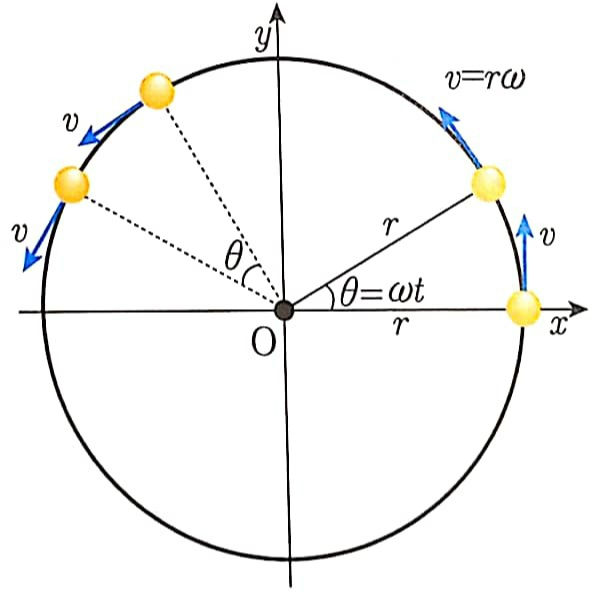
2) 구심 가속도
① 구심 가속도의 방향
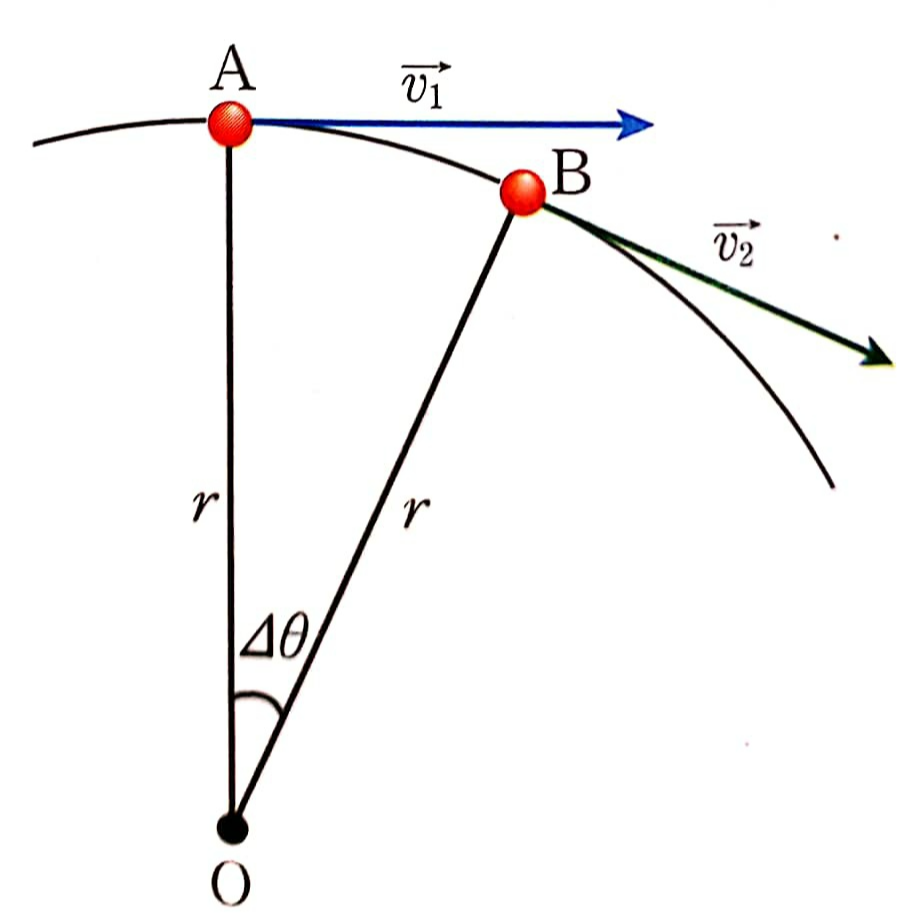
가속도의 방향은 속도 변화의 방향과 같으므로, 속도 벡터의 합성을 이용해 가속도의 방향을 가늠해 볼 수 있습니다.
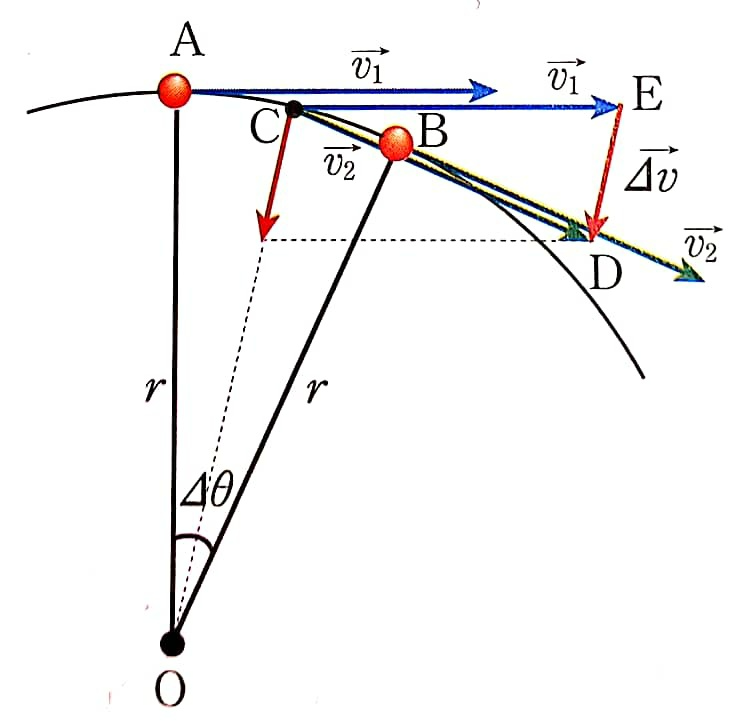
위의 그림에서 확인할 수 있듯이 가속도의 방향은 원의 중심을 향합니다. 즉, 등속 원운동하는 물체의 가속도 방향은 위치와 관계없이 항상 원의 중심을 향합니다. 가속도의 크기를 구해봅시다.
② 구심 가속도의 크기
등속 원운동과 일-에너지 정리
정리하면 구심력의 방향은 구심 가속도의 방향으로써 항상 원의 중심을 향하고 운동 방향에 수직합니다. 구심력의 크기는 뉴턴 제2법칙에 따라 다음과 같이 정의됩니다.

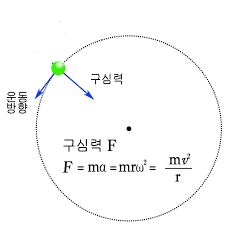
물체에 작용하는 힘, 구심력은 항상 변위에 수직한 방향으로 작용하기 때문에 구심력이 물체에 하는 일이 0이 됩니다. 일 에너지 정리에 따라 물체에 작용하는 힘이 한 일이 0이라면 물체의 운동 에너지는 변화하지 않습니다. 그렇기에 등속 원운동하는 물체의 속력이 일정할 수밖에 없어요. 구심력은 속력을 변화시키지는 않지만, 대신에 운동하는 내내 운동 방향을 변화시키는 역할을 합니다.
실이 끊어졌을 때 물체의 운동과 뉴턴 운동 제1법칙
실이 끊어지면, 더 이상 물체에 작용하는 힘이 없기 때문에 뉴턴 운동 제1법칙에 따라 물체는 정지해 있거나 등속 운동하게 됩니다. 이때 물체는 관성에 의해 실이 끊어지기 직전의 운동 방향과 속력을 유지하는 등속 운동을 합니다.
3) 구심력과 주기, 회전 반지름간의 관계

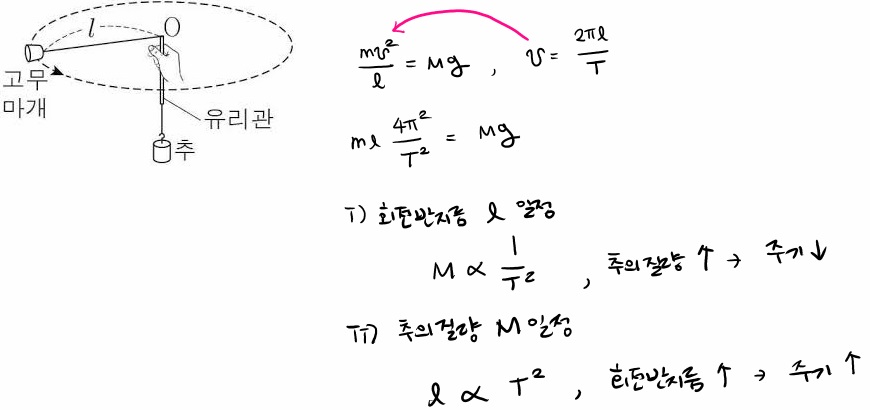
ⓐ고무마개에 작용하는 구심력의 실체
ⓑ회전 반지름이 일정할 때 추의 질량과 주기의 관계
ⓒ추의 질량이 일정할 때 회전 반지름과 주기의 관계
회전목마 - 소코도모
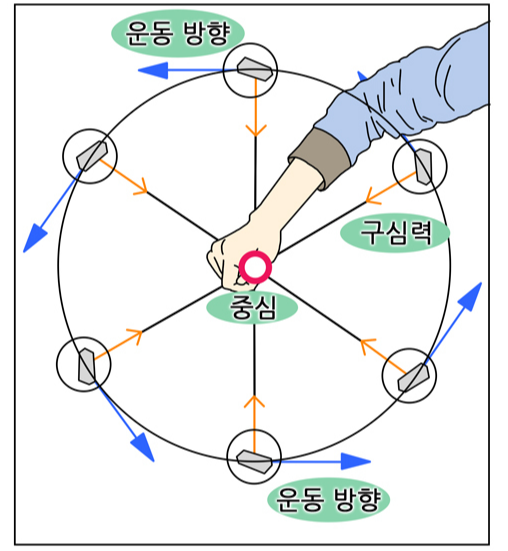
물체가 원을 그리며 돌아가는 이유는 '중심'을 향하는 '구심력'이 물체에 작용하기 때문입니다. 빙빙 돌아가는 물체는 운동 상태를 유지하려는 '관성'에 의해 구심력과 반대 방향을 향하는 '원심력'을 느끼게 됩니다. 그러나 원심력은 실재하는 힘이 아니라 그저 물체가 느끼는 '가상의 힘' 일뿐입니다. 물체를 움직이게 하는 실제적인 힘은 중심을 향하는 구심력뿐이에요.
빙빙 돌아가는 회전목마와 같은 인생이라는 건, 시곗바늘을 따라 돌아가는 나의 모든 시간들에 작용하는 구심력이 있음을 뜻합니다. 목표를 이루기 위한 열망, 오늘보다 더 나아질 내일에 대한 희망, 삶의 중심에 깃든 이 모든 염원들은 시간의 구심력으로써의 역할을 해요. 그 과정에서 나 자신을 삶의 중심으로부터 멀어지게 하는 듯한 '현타'라는 원심력은 필연적으로 따라오는 거고요. 그러나 원심력이 허구이듯 현타 또한 실재가 아닌, 주관적 느낌이 만드는 허구에 지나지 않습니다. 나를 이끄는 실재는 바로 삶의 중심에 깃든 그 모든 염원들이에요.
결국 긴긴 원을 돌아 제자리라는 건, 수없이 흔들려도 중심을 잡고 달려 나가는 여전한 나를 마주하기 위함입니다. 스스로의 초라함을 이겨내며 의미 없어 보이는 일을 5년, 10년, 15년씩 하는 사람들만이 결국에는 자기 분야에서 자기만의 무언가를 가지게 돼요. 그렇기에 부지런히 지나온 어제들을 쌓아가는 사람들의 지나온 기억은 눈부시게 아름답습니다. 오늘도 물리를 통해 인생을 배웁니다.
'물리학II 클립' 카테고리의 다른 글
| 관성력과 등가 원리 (1) | 2022.03.30 |
|---|---|
| 케플러의 법칙과 뉴턴의 만유인력 법칙 (0) | 2022.03.16 |
| 평면 상의 물체 운동 ① {포물선 운동} (0) | 2022.03.11 |
| 회전 운동과 물체의 무게 중심 (0) | 2022.02.28 |
| 힘의 합성과 알짜힘 (0) | 2022.02.28 |









