해당 차시 학습지 파일
학습 목표
이중 슬릿의 간섭 실험을 이용하여 빛의 파장을 구할 수 있다.
빛에 빛을 더해서 어둠을 만들어 낼 수 있다고 누가 상상할 수 있을까!
영의 평전을 쓴 프랑수아 아라고는 광학에 대한 영의 가장 유명한 공헌인 간섭의 법칙에 대해 다음과 같이 우아하게 묘사했습니다. "햇빛 속에서, 광명의 빛이 자유롭게 도달하는 지점에서 어둠을 발견하고 과연 놀라지 않을 사람이 있을까? 빛에 빛을 더해서 어둠을 만들어 낼 수 있다고 누가 상상할 수 있을까!"
빛이 어둠을 빚어낸다는 사실을 밝혀냈듯, 영은 냉담한 현실과 막막한 미래 속에서도 희망의 빛이 존재함을 증명해 냈습니다. 그의 드라마 같은 삶을 물리학으로 노래하는 시간입니다.
빛의 간섭
천재 소년, 언어로 세상을 읽다
1773년 영국 서머싯의 밀버튼 마을에서 태어난 영은 어렸을 때부터 비범한 능력을 드러냈습니다. 그는 두 살 때 글을 유창하게 읽었고, 네 살 무렵에는 성경을 처음부터 끝까지 두 차례 완독했대요. 이처럼 놀라울 정도로 언어에 능숙했던 영은, 10대 시절에 성경의 일부를 열세 개 언어로 번역했다고 합니다. 이러한 타고난 언어적 재능은 훗날 시각과 청각을 넘나들며 자연을 해석하는 독창적인 학문적 감각으로 이어졌습니다.
빛과 소리, 다른 언어 속 같은 진실



영은 뉴턴링 현상을 관악기에서의 간섭 현상으로 비유하며, 빛 또한 소리처럼 파동의 한 종류임을 주장했습니다. 그는 소리의 간섭이 파동의 진동수가 청각적으로 드러난 것이라면, 빛의 색깔은 진동수가 시각적으로 드러난 것이라고 보았습니다. 따라서 뉴턴링 현상은 빛도 소리처럼 간섭한다는 사실을 보여주는 중요한 사례라고 해석했습니다. 이후에 1803년 11월, 영은 런던의 베이커 강연에서 이 주장을 뒷받침하는 가장 강력한 사례를 발표합니다. 그건 바로 이중 슬릿 실험이었습니다.
1) 영의 이중 슬릿 실험

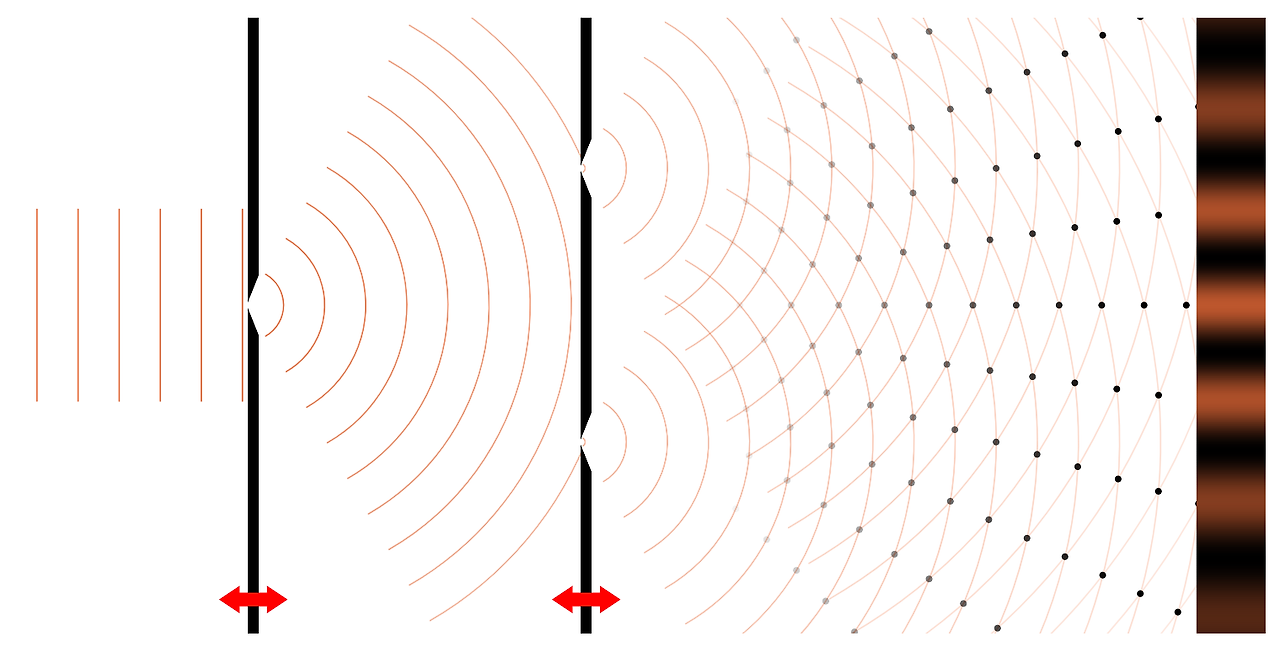
영국의 과학자 영은 이중 슬릿을 통과한 두 빛이 밝은 무늬와 어두운 무늬를 번갈아 만든다는 걸 관찰합니다. 밝은 무늬가 나타나는 곳은 두 빛이 보강 간섭을 일으킨 지점이고, 어두운 무늬가 나타난 곳은 두 빛이 상쇄 간섭을 일으킨 지점입니다. 이처럼 빛도 수면파와 마찬가지로 간섭 현상을 일으켜요. 이러한 빛의 간섭 현상은 빛이 파동임을 입증하는 사례입니다.
https://www.youtube.com/watch?v=WTARZHyxDXc
2) 경로차에 따른 간섭 조건

스크린의 한 지점 P는 중앙의 밝은 무늬로부터 두 번째 밝은 무늬가 생기는 곳입니다. 그리고 θ는 슬릿에서 스크린 중심 O을 향하는 기준선과 슬릿에서 P로 가는 선 사이에 끼인 각입니다. 즉, 기준선에서 얼마나 기울어져 있는지를 나타내는 각도예요. 이때 S1과 S2에서 스크린의 P까지 이동하는 두 빛의 경로 차이는 dsinθ로 근사됩니다.
① 중앙에 밝은 무늬가 생기는 이유
S1과 S2에서 출발한 두 빛이 스크린의 O까지 이동하는 거리가 같기 때문에 두 빛의 경로차는 0이 됩니다. 이는 차수 m이 0일 때의 보강 간섭 조건을 만족시키는 상황이기에, 스크린의 중앙에서는 밝은 무늬가 생깁니다.
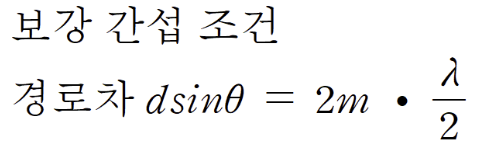
② 차수 m으로 두 빛의 경로차를 찾기
S1과 S2에서 스크린 상의 임의의 지점까지 두 빛의 이동 경로 차에 따라 간섭의 종류가 결정됩니다. 같은 위상의 두 파동의 이동 경로차가 반파장의 짝수 배인 지점에서는 보강 간섭이 나타나고, 반파장의 홀수 배인 지점에서는 상쇄 간섭이 나타납니다.

n번째 밝은(or 어두운) 무늬와 차수 m의 관계
| 밝은 무늬(보강 간섭) 차수 m | 어두운 무늬(상쇄 간섭) 차수 m |
| m=0 (중앙 밝은 무늬) | m=0 (첫 번째 어두운 무늬) - 중앙 밝은 무늬에 바로 이웃함 |
| m=1 (첫 번째 밝은 무늬) | m=1 (두 번째 어두운 무늬) |
| m=2 (두 번째 밝은 무늬) | m=2 (세 번째 어두운 무늬) |

두 번째 밝은 무늬의 차수 m은 2입니다. 따라서 두 빛의 경로차 dsinθ는 2λ예요.
첫 번째 어두운 무늬의 차수 m은 0입니다. 따라서 두 빛의 경로차 dsinθ는 0.5λ예요.

③ 이웃한 무늬 사이의 간격


가상 실험으로 확인하는 이웃한 무늬 사이의 간격
https://javalab.org/youngs_double_slit/
영의 이중 슬릿 - 자바실험실
슬릿들의 간격과 위치를 조절할 수 있습니다. 영의 이중 슬릿 실험 Young의 간섭 실험은 다음과 같습니다. 스크린 A의 작은 구멍 S 0 에서 회절된 빛이 스크린 B에 있는 작은 구멍 S 1 과 S 2 를 지나
javalab.org
단일 슬릿과 결맞음
영의 이중슬릿 실험을 보면 다음과 같은 의문이 들 수 있어요. "왜 이중 슬릿 앞에 단일 슬릿이 있을까? 그냥 S1, S2에 각각 전구 1개씩 두고 실험하면 안 될까?" 이렇게 실험하면 애석하게도 빛의 간섭 현상은 나타나지 않습니다. 두 빛이 결맞지 않기 때문이죠. 단일 슬릿을 두는 이유는 결맞은 빛을 만들기 위해서입니다. '결맞다'라는 말의 뜻은 무엇일까요?

태양, 형광등, 촛불, 백열등을 비롯한 빛들은 열복사 또는 원자 내 전자의 궤도 전이 등등 다양한 광원의 집합체입니다. 다양한 광원에서 방출되는 빛들 각각은 위상이 제멋대로인 데다, 시간에 따른 위상 변화 역시 제멋대로예요. 이런 상태를 '결맞지 않는다'라고 합니다. 결맞지 않는 빛도 빛이기 때문에 간섭을 하지만, 우리 눈은 시간에 따라 불규칙적으로 발생하는 보강 간섭과 상쇄 간섭을 구분하지 못해요. 따라서 S1, S2에 각각 전구 1개씩 두고 실험하면(=두 빛이 결맞지 않아서) 그저 빛 하나에 빛 하나를 더 얹어서 밝기만 밝아지는 결과만 발생할 뿐, 밝고 어두운 규칙적인 띠들은 나타나지 않습니다. 따라서 규칙적인 간섭 띠들을 관찰하기 위해서는 위상차가 시간에 따라 변하지 않는 두 빛으로 실험해야 합니다. 이처럼 위상차가 시간에 따라 변하지 않는 빛을 '결맞은 빛'이라고 해요.
레이저는 고도로 결맞은 빛이기 때문에 레이저로 간섭 실험을 할 때에는 단일 슬릿을 두지 않고도 스크린에서 간섭무늬들을 관찰할 수 있습니다. 그러나 영이 실험을 하던 1801년에는 레이저가 없었기 때문에 빛을 결맞게 해주는 필터, 단일 슬릿이 필요했어요.
어둠 속에서도 빛은 길을 찾아낸다.
1803년, 런던의 베이커 강연. 영은 이중 슬릿 실험을 통해 세상에 선언합니다. “빛도 소리처럼 간섭한다. 빛은 입자가 아니라 파동이다!” 그러나 당시 과학계를 지배하던 것은 뉴턴이 주장하는 빛의 입자설이었습니다. 청중은 침묵했고, 과학자들은 냉담했습니다. 박수갈채 대신 차가운 무시가 돌아왔지요. 끊임없이 이어지는 소모적인 논란에 지친 영은 결국 광학 연구를 내려놓고 다시 의학으로 돌아갔습니다.
하지만 어둠 속에 묻혀버린 그의 주장은 곧 스스로 빛을 발합니다. 프레넬과 후속 연구자들이 영의 실험을 뒷받침하자, 세상은 비로소 눈을 뜹니다. 한때 외면받던 빛의 간섭 법칙은 마침내 19세기 과학의 기념비로 자리 잡았습니다.
빛 - H.O.T
https://www.youtube.com/watch?v=cZrh4mRr-Ig&list=RDcZrh4mRr-Ig&start_radio=1
세상을 지배하던 뉴턴의 권위 아래 묻힐 뻔했던 영의 목소리는 결국 승리했습니다. 어둠이 빛을 삼킨 것이 아니라, 빛이 스스로 어둠을 만들어내며 진리를 증명한 셈이죠. 그러니 세상이 어둠에 둘러싸여 있다 해도 결코 포기하지 마십시오. 지금 여러분의 진실된 노력도 당장은 가로막힐 수 있습니다. 그러나 눈물을 닦고 밝아오는 빛을 맞이하듯, 끝까지 믿고 나아간다면 그 노력은 반드시 빛이 되어 여러분을 우뚝 서게 할 것입니다. H.O.T의 빛을 들으며, 오늘도 물리를 통해 인생을 배웁니다.



