해당 차시 학습지 파일
학습 목표
파동의 간섭을 이해한다.
우리는 모두 자신만의 목표와 꿈을 품고 살아갑니다. 그것이 시험에서 좋은 성적을 거두는 것이든, 원하는 대학에 입학하는 것이든, 혹은 아직 이름조차 붙이지 못한 무언가를 향한 발걸음이든 말이죠. 그러나 목표를 향해 걷는 길은 늘 꽃길만은 아닙니다. 때로는 공부가 버겁고, 노력한 만큼 성과가 보이지 않아 좌절할 때도 있습니다. 밤늦게 책상에 앉아도, 아침에 눈을 떠도, "과연 이게 맞는 걸까?"라는 의문이 마음 한켠을 스칩니다. 그러나 오늘의 물리학은 그 의문이 틀리다고 전합니다.
1. 파동의 간섭

마주 오는 입자끼리는 충돌하게 되면서 서로의 운동 정보(=운동량과 운동 에너지)에 영향을 주기 마련입니다. 하지만 파동의 경우에는 이와 다른 양상을 보입니다.
1) 파동의 중첩과 독립성

마주 오는 파동은 충돌하지 않고 중첩됩니다. 진폭이 yA인 파동 A과 진폭이 yB인 파동 B이 만나게 되면 진폭이 yA + yB인 파동이 되는데요. 이를 파동의 중첩이라 합니다.


파동이 중첩될지라도 서로가 서로에게 영향을 주지 않기 때문에 원래 파동이 갖던 각각의 파장과 주기 그리고 진폭은 변하지 않아요. 따라서 각 파동은 자신의 속력을 유지한 채 다시 원래의 파형으로 돌아와서 각자 가던 길을 갑니다. 이처럼 파동은 독립적이에요. 이러한 파동의 성질, 중첩과 독립이 간섭이라는 파동만이 갖는 고유한 현상을 일으키는 원인입니다.
2) 간섭의 종류
파동이 중첩되면 원래 파동보다 진폭이 커지거나 작아집니다. 이에 따라 간섭은 두 종류로 구분돼요.

| 보강 간섭 | 상쇄 간섭 |
| 진동수와 파장이 같은 두 파동이 마루와 마루, 골과 골이 만나도록 중첩되어 합성파의 진폭이 커지는 현상 >두 파동이 같은 위상으로 중첩되는 경우 |
진동수와 파장이 같은 두 파동이 마루와 골, 골과 마루가 만나도록 중첩되어 합성파의 진폭이 줄어드는 현상 >두 파동이 반대 위상으로 중첩되는 경우 |
진폭과 위상의 차이
파동에는 진폭과 위상이라는 물리량이 있는데요. 얼핏 비슷한 개념 같지만 엄밀히 따지면 달라요. 진폭이란 진동 중심에서 마루 또는 골까지의 길이, 즉 공간 개념이고요. 위상이란 진동의 타이밍, 즉 시간 개념입니다.
2. 수면파의 간섭
앞서 살펴봤듯이 두 파동의 위상 차이가 간섭의 종류를 결정했습니다. 위상차가 0º인 경우 보강 간섭, 위상차가 180º인 경우 상쇄 간섭이 나타났는데요. 간섭의 종류를 결정하는 또 다른 디테일이 있습니다.
두 개의 공을 동일한 박자와 세기로 수면을 쳐줄 때 생기는 두 개의 수면파는 위상과 진폭이 서로 같습니다. 따라서 수면파들은 보강 간섭만 일으켜야 하는데요. 실제로는 두 개의 수면파가 보강 간섭하여 수면이 계속 진동하는 지점이 있고, 상쇄 간섭하여 수면이 잔잔한 지점 또한 발생합니다. 왜 그럴까요?
간섭이 나타나는 지점에서 수면파의 진폭 변화

| 보강 간섭하는 지점 | 상쇄 간섭하는 지점 | |
| 수면파 | 최고 수면과 최저 수면이 번갈아 나타남 | 수면의 높이가 변하지 않음 |


그 이유는 두 파원(=공으로 수면을 쳐주는 곳)으로부터 해당 지점까지의 경로 차이(=두 수면파가 해당 지점에 이를 때까지 이동한 거리의 차이)가 해당 지점에서 두 파동의 위상 차이를 결정하기 때문입니다.
1) 보강 간섭

S2에서 p까지 수면파가 한 파장 λ을 이동할 때, 위상이 같은 또 다른 수면파는 S1에서 p까지 두 파장 2λ을 이동한다고 가정할게요. 이때 두 파동의 경로가 한 파장 λ만큼 차이가 나는데요. 이처럼 두 파동의 경로 차이 δ가 파장의 정수배(=반파장의 짝수배)에 해당되는 지점 p에선 두 파동이 같은 위상으로 만나기 때문에 보강 간섭이 일어납니다.

그림에서 보강 간섭하는 지점을 찾기

P, Q 중에 보강 간섭하는 지점은 P입니다. 그 이유는 마루와 마루(혹은 골과 골)가 만나는 곳이기 때문이죠. 경로차로도 확인할 수 있습니다. S1P = 3λ, S2P = 4λ, 경로차∣S1P - S2P ∣= λ = 2 ⋅ λ/2, 즉 경로차가 반파장의 짝수배에 해당하는 곳이기에 P 지점에서 보강 간섭을 합니다.
2) 상쇄 간섭

S2에서 p까지 수면파가 한 파장 λ을 이동할 때, 위상이 같은 또 다른 수면파는 S1에서 p까지 1.5 파장 1.5λ을 이동한다고 가정할게요. 이때 두 파동의 경로가 반 파장 λ/2만큼 차이가 나는데요. 이처럼 두 파동의 경로 차이 δ가 반파장의 홀수배에 해당되는 지점 p에선 두 파동이 반대 위상으로 만나기 때문에 상쇄 간섭이 일어납니다.
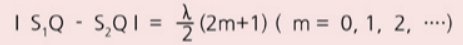
그림에서 상쇄 간섭하는 지점을 찾기

P, Q 중에 상쇄 간섭하는 지점은 Q입니다. 그 이유는 마루와 골이 만나는 곳이기 때문이죠. 경로차로도 확인할 수 있습니다. S1Q = 4λ, S2Q = 2.5λ, 경로차∣S1Q - S2Q ∣= 1.5λ = 3 ⋅ λ/2, 즉 경로차가 반파장의 홀수배에 해당하는 곳이기에 Q 지점에서 상쇄 간섭을 합니다. 상쇄 간섭하는 지점을 이은 선을 마디선이라고 합니다.
두 파동의 위상이 반대인 경우의 경로차에 따른 간섭 조건
ⓐ 보강 간섭
경로차 δ = (2m+1) ½ λ , m=0,1,2.....
ⓑ 상쇄 간섭
경로차 δ = (2m) ½ λ , m=0,1,2.....
Maybe Tomorrow - DAY6
https://www.youtube.com/watch?v=IrI-1lyIGKM&list=RDIrI-1lyIGKM&start_radio=1
위상이 같은 두 수면파가 만나면, 물결은 더 높아지기도 하지만 동시에 더 깊어지기도 합니다. 우리의 삶도 마찬가지예요. 어떤 목표는 우리를 웃게도 하지만, 때로는 바닥 끝까지 끌어내릴 만큼 힘들게 만들기도 합니다. 그 고통은 어쩌면 그 목표가 우리의 본질과 결을 맞추었기에 생기는 보강 간섭의 일부일지도 모릅니다. 그렇기에 깊게 내려갔다면 부득불 더 크게 솟아오를 수 있는 법. 결이 맞지 않는 목표였다면, 아마 큰 성취감도 큰 좌절도 없이 상쇄 간섭처럼 잔잔하기만 했을 것입니다.
내일이 되면 오늘보단 따뜻하겠지. 살을 에는 이 추위가 좀 잦아들겠지. 내 맘을 감싸 줄 봄을 기다려
그러니 오늘이 혹독하게 춥더라도 포기하지 마세요. 지금의 추위는 봄을 향한 과정일 뿐입니다. 파도처럼 몰아치는 어려움 속에서 그 물결은 당신을 삼켜버리는 것이 아니라 더 높이 들어 올리고 있습니다. 언젠가 가장 높은 파도 위에서, 우리는 이 모든 물결이 자신을 빚어준 과정이었다는 걸 깨닫게 될 것입니다. DAY6의 Maybe tomorrow를 들으며, 오늘도 물리를 통해 인생을 배웁니다.
'물리학II 클립' 카테고리의 다른 글
| 파동의 회절 (4) | 2022.08.25 |
|---|---|
| 영의 이중슬릿 실험으로 알아보는 빛의 간섭 (0) | 2022.08.22 |
| 전자기파의 발생과 수신 (1) | 2022.08.16 |
| LC 회로의 특성 (0) | 2022.08.11 |
| 유도 기전력 및 상호 유도 (0) | 2022.06.21 |



