자유 낙하하는 물체들이 같은 높이에서 떨어진다면, 질량과 관계없이 바닥에 닿기까지 소요되는 시간은 동일하다. 이는 중력에 의한 현상으로써 지금 보면 너무나 당연한 사실이기에 아리스토텔레스의 아래와 같은 주장을 보면 콧방귀를 뀔 수 있다.

일찍이 고대 그리스에서 잘 나가던 철학자인 아리스토텔레스는 사색과 관찰을 통해 수많은 업적을 이뤄냈다. 그가 제시한 대표적 이론 중에는 세상은 물, 불, 흙, 공기 이렇게 4가지 원소로 이루어졌다는 '4원소설'이 있다. 지금에서 보면 굉장히 얼탱이 없지만 4원소설은 아리스토텔레스라는 명성에 힘입어 연금술과 플로지스톤론에 이르기까지 과학계에 지대한 영향을 미치며 오랫동안 과학의 발목을 붙잡는다.(동시대의 데모크리토스의 원자론은 명성이 후달린 탓에 ㅈㅂ취급 당함.)
1. 연역, 규칙을 통한 성찰

아리스토텔레스 하면 빼먹을 수 없는 '삼단논법'은 대표적인 연역적 추리이다. 연역적 추리는 아리스토텔레스가 자연 현상을 분석할 때 애용했던 사색법이다.
1) 연역의 구조
연역은 과학 법칙과 이론들로부터 자연 현상을 설명할 때, 다음과 같은 설명 구조를 가진다.

- 법칙과 이론들(전제1)
ex) 물체의 운동 방향은 변하지 않고 속력이 점점 느려진다면, 그 물체에는 운동 반대 방향으로 알짜힘이 작용하고 있다.
- 초기 조건들(전제2)
ex) 수직 위로 던진 물체는 올라가는 중, 방향이 변하지 않고 속력이 점점 느려진다.
- 자연 현상에 대한 설명(결론)
ex) 따라서 수직 위로 던진 물체는 올라가는 중, 물체에는 아래 방향으로 알짜힘이 작용하고 있다.
2) 연역의 예시 -해왕성 발견-

19세기에 천문학자들은 천왕성의 궤도가 뉴턴 법칙으로 계산된 궤도에서 조금 벗어나 있음을 발견하고 한동안 고민에 빠졌다. 뉴턴의 법칙이 틀린 것일까? 아니면 아직 발견되지 않은 다른 행성의 중력 때문에 정상적인 궤도에서 벗어난 것일까? 프랑스의 천문학자 위르뱅 르베리에는 뉴턴의 운동법칙이 옳다는 가정하에 새로운 행성의 위치를 계산했고, 이 행성은 1846년에 르베리에가 계산했던 위치로부터 1도 이내의 거리에서 발견되어 '해왕성'으로 명명되었다. 이것은 뉴턴의 운동 법칙을 입증한 강력한 증거이자 '오직 수학 계산만으로 천체의 위치를 예측한' 최초의 사례이다.

3) 연역의 한계
아리스토텔레스는 4원소설을 기반으로 물체의 낙하운동을 설명한다. 결국 '4원소설'이 쏘아 올린 포탄은 결국 '무거운 돌이 가벼운 돌보다 빨리 떨어진다.'는 불발탄이었다. 이처럼 잘못된 전제는 잘못된 결론을 도출할 수밖에 없다. 더 큰 문제는 전제가 참인지 거짓인지 판가름하는 데 연역적 추리만으로는 한계가 있다는 점이다.

그렇다고 아리스토텔레스를 돌대가리 취급하는 것은 옳지 않다. 그 당시엔 '힘'이란 개념 자체가 없었기 때문이다. 그래서 물체가 힘에 의해 움직인다는 생각을 일절 하지 못했다. 언감생심 중력에 의해서 물체가 떨어진다고 생각이나 할 수 있었을까? '힘'은 아리스토텔레스 사후, 근 2000년이 지나고 뉴턴이 데뷔시킨 개념이었다. 힘은 'F=ma, 뉴턴 운동 법칙'이란 기가 막힌 퍼포먼스를 선보이며 '물체의 운동을 설명'하는 화려한 쇼케이스를 보여줬다. 그러나 기가 막힌 퍼포먼스 배후엔 뛰어난 안무가가 있는 법. 바로 베이컨이다.
1. 귀납, 경험을 통한 성찰

베이컨은 아리스토텔레스의 삼단논법을 대체해서 보편적인 진리를 찾아내는 새로운 방법으로 '귀납'을 제시했다. 진정으로 참인 지식을 얻기 위해 개별 사건들에서 보편적인 지식을 얻어야 했기 때문에 '실험'이란 실제적인 확인 작업이 매우 중요시되었다. 즉, 베이컨의 귀납적 탐구는 과거의 사색적인 성격의 과학 활동을 실제적인 방법을 동원하여 유용한 결과물을 창출하는 방향으로 전환한 셈이다.
1) 귀납의 구조
귀납적 탐구는 자연현상에서 관찰한 결과들을 종합해서 결론을 이끌어내는 과정이다.

순수한 물을 가열하였을 때 끓는 온도를 측정하면 100℃라는 관찰 사실을 얻을 수가 있다. 10번 또는 100번의 관찰이 모두 100℃에서 끓었다면, 이제 우리는 '모든 순수한 물은 항상 100℃에서 끓는다'라는 보편 법칙을 얻어낼 수 있다. 이처럼 10번 또는 100번의 관찰 사실만으로 '모든 순수한 물'이 '항상 100℃에서 끓는다'는 주장을 할 때 우리는 귀납을 한 것이다.
2) 귀납의 예시 -패러데이 법칙-
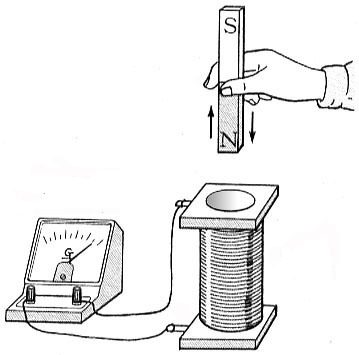
패러데이는 코일에 자석을 넣었다 뺐을 때 검류계 바늘이 움직이는 것을 발견했다. 검류계 바늘이 움직인다는 건 코일에 연결된 전선에 전류가 흐른다는 걸 의미한다. 이는 자석의 자기장이 코일에 흐르는 전류를 유도한 결과임에 틀림없다. 패러데이는 다음과 같은 수많은 관찰 사실을 종합하여 다음과 같이 패러데이 법칙을 완성했다.


3) 귀납의 한계
몇 개의 한정된 관찰 사실들로부터 일반화된 법칙을 찾아내는 과정에서 어떻게 한정된 수의 관찰 사실들 만으로 '언제나, 모든, 항상'이라는 보편 법칙을 주장할 수 있겠는가에 대한 논의가 바로 귀납의 한계이다.
과학을 과학답게
머릿속 관념이 아니라 구체적 사실에서 진리를 구해야 한다는 베이컨의 정신이 과학혁명의 문을 열었다. 그 문으로 뉴턴이 입장하며 종래의 사변적 경향에 제동이 걸리고, 과학의 실용적 가치가 고양되었기에 철학인 듯 철학 아닌 철학 같은 과학이 비로소 과학다워졌다.
'사이언스토리텔링' 카테고리의 다른 글
| 용수철 진자와 LC 회로에서의 단진동 (0) | 2023.10.08 |
|---|---|
| 거꾸로 오르는 바퀴 (역학적 에너지 보존 법칙, 질량중심) (0) | 2023.08.14 |
| '우주배경복사'처럼 어디에나 존재하는 내 안의 잠재력 (1) | 2023.03.30 |
| 무게중심과 외래 바다 생물 (2) | 2023.02.10 |
| 블랙홀과 중국 (0) | 2023.02.09 |




사이언스토리텔러님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.