물리학Ⅰ 전개도

2023.04.27 - [2023 물리학I 톺아보기] - 지려버리는 불장난, 증기기관 (자연을 통제하고 활용한 인류①)
지려버리는 불장난, 증기기관 (자연을 통제하고 활용한 인류①)
https://www.youtube.com/watch?v=lnhQivIp8uA 지려버리는 불장난, 증기기관 '증기기관'은 '불장난'이다. 그저 철없는 아이들의 바지를 지리게 했던 불장난과는 차원이 다르다. 그 이유는 증기기관은 인류 문
gooseskin.tistory.com
판서 조직도

목표 기출 문제
14년도 9월 모평 물리1 5번

답: 4번
14년도 4월 학평 물리1 3번

답: 4번
1. 기체가 하는 일과 내부 에너지
1) 기체 분자 운동에 의한 일
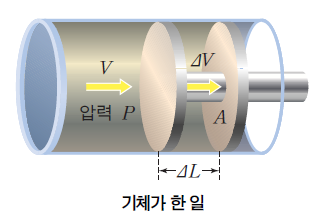
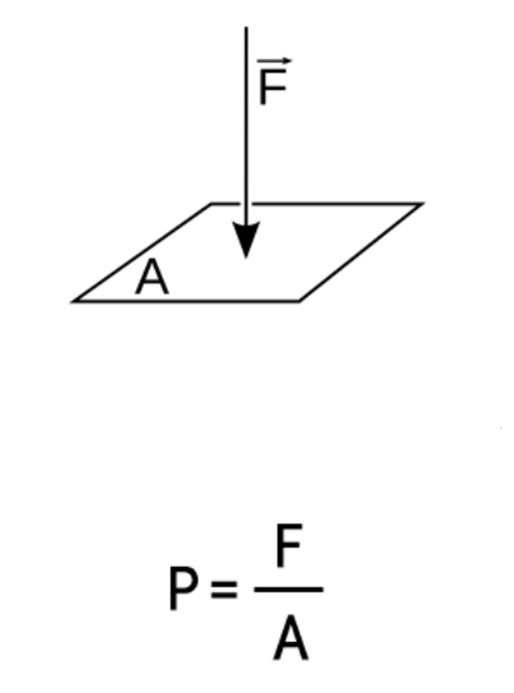
압력(P)은 단위 면적(A)에 수직으로 작용하는 힘(F)이다. 따라서 기체의 압력 P에 피스톤의 면적 A를 곱하면 기체가 피스톤에 미치는 힘 F가 된다. 이렇게 힘 F(=PA)를 가해서 피스톤이 거리 △L만큼 움직였다면 기체는 피스톤에 'W = F△L = PA△L = P△V'만큼의 일을 해준 것이다.
| 기체가 팽창할 때(△V>0) | 기체가 수축할 때(△V<0) | 압력과 부피 모두 변할 때 |
 |
 |
 |
| 기체가 외부에 W만큼의 일을 한다. (W>0) |
기체가 외부에서 W만큼의 일을 받는다. (W<0) |
부피-압력 그래프의 아래 면적이 일의 양이다. |
2) 내부 에너지
기체 분자의 역학적 에너지를 기체 분자의 '내부 에너지'라고 한다. 물리학1에선 주로 이상(ideal )기체의 열현상을 다루는데, 이상 기체 분자끼리는 서로 상호 작용을 하지 않기 때문에 퍼텐셜 에너지가 무시된다. 따라서 이상기체의 내부 에너지는 곧 기체 분자의 운동 에너지라고 생각하면 된다.
①절대온도 T
열역학에서는 우리에게 익숙한 온도 단위인 섭씨온도 [℃]보다는 절대 온도[K]를 사용한다. 섭씨온도를 절대 온도로 환산하려면 섭씨온도에 273을 더하면 된다. '절대온도 T[K]= 섭씨온도[℃] + 273'
켈빈의 인맥
절대 온도의 단위 K(켈빈)은 절대 온도 체계를 정립한 영국 과학자 윌리엄 켈빈 경의 공로를 인정해 그의 이름을 따서 정한 것이다. 그러나 이것 말고도 켈빈은 사람과 사람사이에 다리를 놔줌으로써 물리학에 혁혁한 공을 세웠다.
지금 우리가 누리는 첨단 정보통신의 기술은 상대성 이론의 산물이다. 아인슈타인의 상대성 이론은 전자기 방정식을 완성한 맥스웰이 없었으면 불가능했다. 맥스웰 방정식은 전기와 자기의 관계를 다룬 패러데이 이론이 없었으면 불가능했다. 그런 맥스웰에게 패러데이를 소개한 사람이 바로 켈빈이다. 켈빈이 패러데이를 맥스웰에게 소개하지 않았다면 맥스웰 방정식, 상대성 이론이 등장하는 데 더 오랜 시간이 걸리지 않았을까?
②온도와 내부 에너지의 관계
기체 분자의 운동 에너지는 절대 온도에 비례한다. 기체의 온도가 높다는 건 그만큼 기체 분자의 운동이 활발하다는 뜻이고, 기체의 온도가 낮다는 건 그 반대다. 따라서 기체 분자의 운동 에너지, 즉 기체의 내부 에너지는 온도에 비례한다. 'U(내부 에너지) ∝ T(절대 온도)'
따라서 기체의 온도가 높아질 때(△T>0) 기체의 내부 에너지는 증가(△U>0)하고, 기체의 온도가 낮아질 때(△T<0) 기체의 내부 에너지는 감소(△U<0)한다.
상태 방정식, PV=NKT
상태 방정식은 물리학1에서 배우지 않지만 알아놓으면 정말 유용하게 쓰인다. 사실 처음 보는 것도 아니다. 중학교 과학 시간에 공부했던 보일-샤를 법칙이 이 상태 방정식을 근거로 설명된다.


밀폐된 용기의 기체 분자수 N은 변함이 없고, k는 상수이니까 항상 일정한 값이다. 따라서 밀폐된 용기에 있는 기체의 PV/T 값은 상수이다. 이는 보일-샤를 법칙을 완벽히 설명한다.

2. 열역학 제1법칙
1) 사실은 에너지 보존 법칙


밥을 먹고(Q) 몸을 움직이면(W) 그 차이만큼의 에너지(△U)가 남는다. '△U = Q - W'
어떤 계(system)의 내부 에너지 변화량(△U)은 계에 출입한 열(Q)에서 기체가 한 일(W)을 뺀 양과 일치함을 알 수 있다. 이 관계를 설명하는 법칙이 '열역학 제1법칙'이다. 식을 정리하면 다음과 같다. 'Q=△U+W'
사실 열역학 제1법칙은 열에너지와 역학적 에너지를 포함한 보다 일반화된 '에너지 보존 법칙'이다.
부호 규칙
| Q>0 계가 열을 흡수 |
Q<0 계의 열이 방출 |
| △U>0 계의 온도 증가 |
△U<0 계의 온도 감소 |
| W>0 기체가 외부에 일을 함 |
W<0 기체가 외부로부터 일을 받음 |
2) '상태 방정식'과 '열역학 제1법칙'으로 분석하는 열역학 과정
①등압 과정
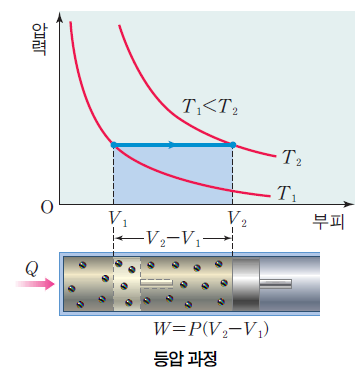
등압 과정시 압력 P가 변하지 않는다. 열역학 제1법칙 Q = △U + W(P△V)에 의해서 열 출입이 내부 에너지와 부피의 변화에 기여하는 과정이다.

반대의 과정에서는 (압력이 일정하지만 부피가 줄어드는 경우) △V<0 이므로 W<0 이고, 온도가 감소하므로 △U<0이어서 Q<0 이게 된다. 이 경우는 계가 열을 방출한다.
②정적 과정

정적 과정시 부피 V가 변하지 않는다. 열역학 제1법칙 Q = △U + W(P△V) , 즉 W=0이 된다.
이 과정에서는 열 출입이 내부 에너지 변화에만 기여한다.

반대의 과정엔 온도가 감소하므로 계가 방출한 열만큼 내부 에너지가 감소한다.
③단열 과정

단열 과정은 외부로의 열출입이 없는 열역학 과정이다 따라서 Q=0이다. 열역학 제1법칙 Q = △U + W(P△V) 에 의해서 △U = - W이다.즉 기체가 외부에 일을 하면 (부피가 팽창하면) 계의 온도는 낮아지고, 기체가 외부로부터 일을 받으면 (부피가 수축하면) 계의 온도는 높아진다.

비행운 - 문문
어제와 오늘의
온도가 너무 달라서
비행운이 만들어졌네
내가 머물기에
여기는 너무 높아서
한숨 자국만 깊게 드러났네

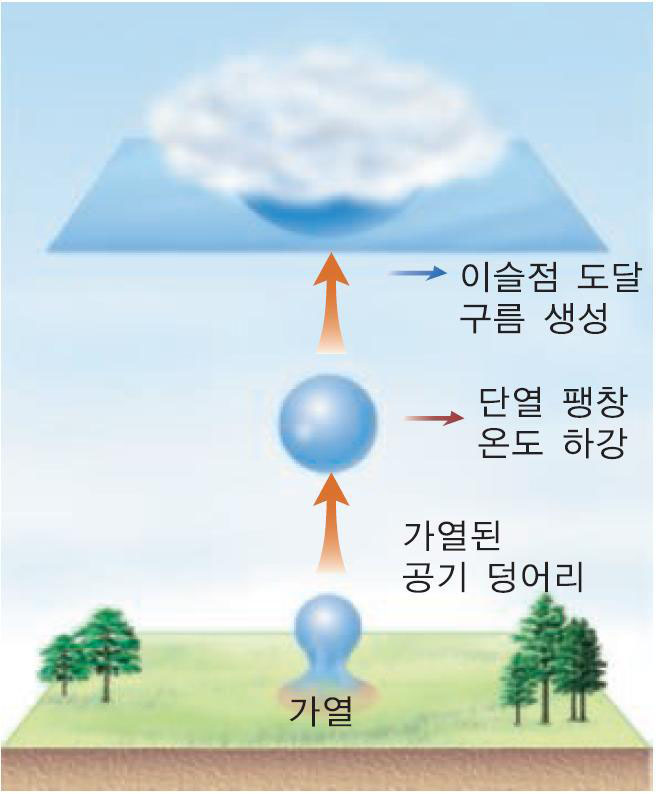
비행운은 '단열 팽창'과 관련된 현상으로 구름이 생기는 이유와 동일하다. 단열 팽창이란 외부의 열 출입이 없는 상태에서 기체가 외부에 일을 하여 기체의 온도가 떨어지는 열역학 과정을 일컫는다. 비행기 내부의 제트엔진 속 좁은 공간에 있던 공기들이 대기 중으로 분출되면 공기의 기압이 낮아지면서 부피가 커진다. 워낙 빨리 이루어지는 과정이다 보니 외부의 열 출입이 제한된다. 따라서 기체 스스로 부피를 팽창시키느라 자신의 에너지를 온전히 다 써버리기 때문에 기체의 온도가 낮아지게 된다. 이로 인해 제트엔진에서 배출된 배기가스의 수증기가 자그마한 물방울로 응결된다. 비행운은 이 응결된 물방울(빙정) 주위로 다른 수증기가 모여들어 생긴 기나긴 구름이다.

해와 달이 떠 있는 높은 곳에 가기 위해 비행기는 힘차게 비상한다. 뜨거운 이상을 품은 채로.
하지만 비행기는 마주하게 된다. 그곳은 머물기에 너무 높다는 사실을 알려주는 차갑고 혹독한 현실을.
결국 비행기는 현실과 타협하게 된다. 큰 욕심을 부리지 않고 자신이 머물기에 적당한 곳만을 배회하기로.
한때 바랐던 곳을 그저 바라만 볼 수밖에 없는 씁쓸함에 내쉬어지는 비행기의 한숨 자국은 비행운으로 남는다.
결국 '비행운'은 한때 누구 못지않게 뜨거웠지만 냉혹한 현실에 짜게 식어가는 우리의 인생을 자조하는 노래인 셈이다. '비행운'은 과거의 뜨거웠던 이상과 냉혹한 현실의 온도차가 만들어낸 우리의 자욱한 한숨 자국이다.

꿈을 이룬 멋진 사람이 되고 싶다.
바라던 대로 이루어졌으면 좋겠다.
가급적 빨리
누구나 한 번쯤은 가져 봤을 희망 사항일 것이다. 나도 그랬다. 기왕이면 빠른 게 좋다는 생각에 앞만 보고 달렸다. 그저 앞에 있는 이상만을 주시하며 달리는 데 주변 풍경이 눈에 들어올 리 만무했다. 그렇게 시야가 좁아지다 보니 욕심은 더 커져갔고, 그런 욕심이 만드는 허울은 현실을 똑바로 보지 못하게 했다. 그럴 때마다 이상과 현실 간의 괴리를 마주하는 순간은 어김없이 찾아왔다. '얼마나 더 빨리 달려야 하는 것인가'라는 현타가 오면서 나 자신이 초라해지다가도 문득 그런 생각이 들었다. '빨리빨리'에 매몰되어 미래를 담보로 현재를 희생시켰던 나 자신이 안쓰럽다는 뭐 그런 거.
빨리 일어나는 단열 팽창 과정으로 발생한 온도 차가 만드는 비행운
이상과 현실의 괴리를 빨리 메우고 싶은 욕심이 만드는 한숨 자국
비행운은 미래를 담보로 현재를 희생시킨 꼬마의 한숨 자국이자 나의 한숨 자국이었다.
빠르게 가려고 하지 말라, 대신 일찍 시작하라.

그런 나에게 '나의 하루는 4시 30분에 시작된다.'는 큰 깨달음을 준 고마운 책이었다. 빨리 되려 하지 말고 남보다 일찍 시작하는 사람이 돼라는 저자의 메시지가 내게 큰 울림으로 다가왔다. 더 이상 미래를 담보로 현재를 희생시키지 않아도 되는 법을 가르쳐 준 책이었다.
현재가 갖는 소중한 가치를 깨닫고, 보다 더 현명하게 현재를 보낼 수 있는 체계적인 시간 관리법을 터득하여 비행운 너머 무지개를 볼 수 있는 여유 있는 사람이 됐으면 좋겠다. 여러분도 나도.
도전 기출 문제
19년도 6월 모평 물리1 16번
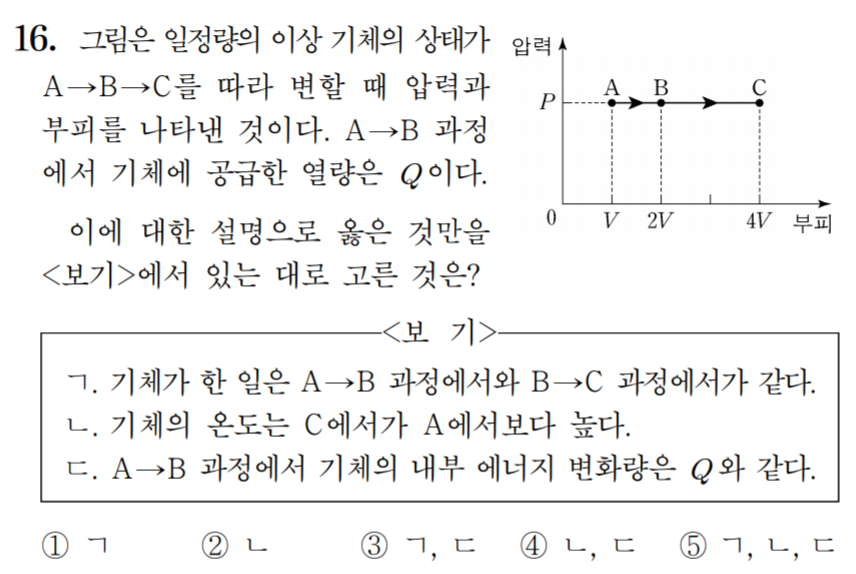
답: 2번
2023.05.04 - [2023 물리학I 톺아보기] - 열역학 법칙② (엔트로피, 열기관의 열효율)
열역학 법칙② (엔트로피, 열기관의 열효율)
2023.05.03 - [2023 물리학I 톺아보기] - 열역학 법칙① (PV=NkT, 열역학 과정) 열역학 법칙① (PV=NkT, 열역학 과정) 물리학Ⅰ 전개도 2023.04.27 - [2023 물리학I 톺아보기] - 지려버리는 불장난, 증기기관 (자연
gooseskin.tistory.com
'2023 물리학I 톺아보기' 카테고리의 다른 글
| [엔트로피] 인생의 회전목마 (2) | 2023.05.08 |
|---|---|
| 열역학 법칙② (엔트로피, 열기관의 열효율) (0) | 2023.05.04 |
| 지려버리는 불장난, 증기기관 (자연을 통제하고 활용한 인류①) (2) | 2023.04.27 |
| 일과 에너지Ⅱ(평형점, 키워드별 기출문제 풀이) (0) | 2023.04.11 |
| 일과 에너지(일-에너지 정리, 운동 에너지, 퍼텐셜 에너지, 역학적 에너지 보존) (0) | 2023.03.21 |



