gooseskin.tistory.com/154
상호작용하는 두 힘의 관계(뉴턴 운동 3법칙)
gooseskin.tistory.com/152 힘, 질량, 가속도의 관계를 정리한 뉴턴 gooseskin.tistory.com/147 여러 가지 물체의 운동 학습목표 여러 가지 물체의 운동 사례를 찾아 속력의 변화와 운동 방향의 변화에 따라 분
gooseskin.tistory.com
학습목표
물체의 1차원 충돌에서 충돌 전후 운동량 보존을 이용하여 속력의 변화를 정량적으로 예측할 수 있다.
충격량과 운동량의 관계를 이해하고, 일상생활에서 충격을 감소시키는 예를 찾아 설명할 수 있다.
핵심 키워드 조직도

※ 학습 목표 및 핵심 키워드 조직도 분석 (밑의 '더보기'를 클릭)
서로 다른 두 물체 사이에 작용하는 두 힘은 작용과 반작용 관계를 이루고 있다는 '뉴턴 운동 3법칙'이 '운동량 보존 법칙'이라는 새로운 언어로 표현되는 과정을 확인해본다. 이때 운동량과 충격량의 관계를 이용하여 충격력을 조절할 수 있는 방법의 원리도 확인할 것이다.
1. 운동량 보존 법칙
운동량 보존 법칙은 사실 뉴턴 운동 3법칙의 다른 표현일 뿐이다.

두 물체가 충돌하는 시간(△t) 동안 서로에게 작용하는 힘은 작용 반작용 관계에 있기 때문에 크기가 같고, 방향은 서로 반대다.

정리하면 충돌 전후로 두 물체가 갖는 어떤 물리량이 보존된다더라. 그게 P라는 물리량이고, 과학자들은 P를 운동량이라고 정의한 셈이다. 즉 충돌하는 두 물체 사이에서 발생하는 힘들이 '뉴턴 운동 3법칙'을 따르기 때문에 물체 사이에서 필연적으로 보존되어야 할 물리량이 있었고, 그 물리량에 '운동량'이라는 이름을 붙여준 것뿐이다.
①보존되는 것과 보존되지 않는 것 구별하기
착각하지 말아야 할 것은 충돌 전후에 물체 각각의 운동량은 보존되지는 않는다는 점이다.

A는 충돌하는 순간 B로부터 FA라는 힘을 받고, B는 충돌하는 순간 A로부터 FB라는 힘을 받는다.
즉, A에겐 FA라는 알짜힘이 작용했고, B에겐 FB라는 알짜힘이 작용했다는 것이다. 각각은 힘을 받은 만큼 운동량이 변하였기 때문에 충돌 전후 각각의 속도가 변했다.

다만 A와 B의 운동량 합은 보존이 된다. A와 B를 묶은 전체 시스템 입장으로 바라보자. 충돌 전 A와 B는 등속도 운동을 하고 있었으므로 'A-B 시스템'에 작용하는 알짜힘은 0이었다. 충돌하는 순간 'A-B 시스템' 내부에 발생하는 힘들은 상쇄된다. 충돌 후 역시 A와 B가 등속도 운동을 하고 있으므로 'A-B 시스템'에 작용하는 알짜힘은 0이 된다.
따라서 'A-B 시스템'엔 전체적으로 작용하는 알짜힘이 0인 상태이므로 'A-B 시스템' 총운동량엔 변함이 없다.
②운동량 보존 법칙이 적용되는 예를 산술적으로 살펴보기



2. 충격량
①충격량의 정의

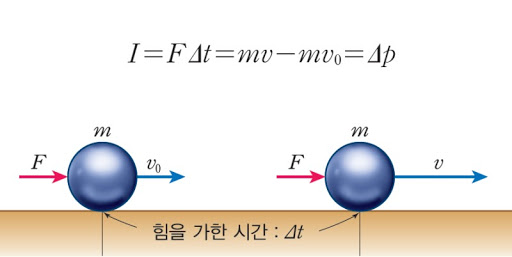
m에게 △t동안 F가 작용하면 운동량이 △P만큼 변하게 되는데, △P를 충격량(I)라 정의한다.
②△P가 일정할 때의 상황







모두 뭔가 움직이던 물체들이 최종적으로 정지하게 되는 상황이다.
야구할 때 글러브를 안 끼면 손바닥이 아작 나고 → 맨손으로 받는 것보다 공이 정지하기까지 오래 걸림
태권도할 때 낙법을 쓰지 않으면 척추와 무릎 관절이 아작 나고 → 낙법을 쓰면 정지하기까지 오래 걸림
번지점프할 때 고무줄이 아닌 밧줄을 쓰면 몸이 아작 나고 → 고무줄로 낙하할시 정지하기까지 오래 걸림
택배 상자에 포장재를 넣지 않으면 상품이 아작 나고 → 정지하기까지 오래 걸림
자동차에 범퍼나 에어백을 장착하지 않으면 인생이 아작 난다. → 정지하기까지 오래 걸림
우리가 원하는 건 모든 물체들이 정지하기까지 힘을 덜 받는 것이고, 최종적으로 우리가 행복해지는 데 있다. 뭐가 됐든 어떤 속도로 움직이던 물체가 최종적으로 정지하는 상황이므로 운동량의 변화량(△P)이 일정한 상황이다.

즉 힘이 작용하는 시간을 최대한 길게 해줌으로써 힘 F를 줄일 수 있다.
③힘 F를 오랜 시간동안 작용함으로써 충격량을 늘리는 상황


왼쪽의 기관포보다는 오른쪽의 자주포의 사정거리가 훨씬 길다. 멀리 날아간다는 것은 자주포 포탄이 가지는 운동량이 기관포의 포탄이 가지는 운동량보다 더 크다는 걸 의미한다.(속도가 더 빠르니)
똑같은 연료의 폭발력(=포탄에게 작용하는 힘 F가 같다.)으로 포탄이 날아가는 건데 왜 둘의 사정거리는 다를까?
그 이유는 포신의 길이가 길수록 힘 F가 작용하는 시간(△t)이 그만큼 길어지기 때문이다.

똑같은 세기로 바람을 불어도 좀 더 긴 빨대를 이용하면 발사체를 멀리 날릴 수 있다. 그 이유를 댓글로 달아보자.
3. 달걀을 방석에 떨어뜨리면 깨지지 않는 이유
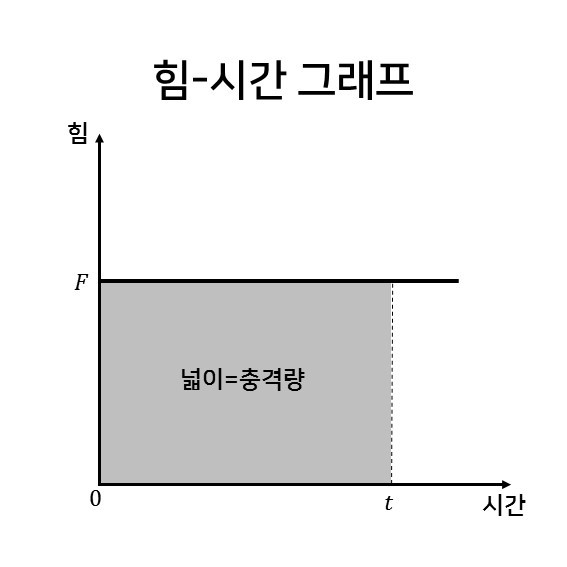
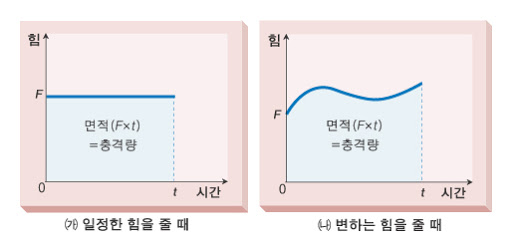
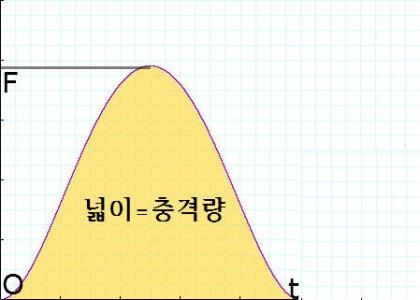
운동량 변화량 즉, 충격량이 힘과 시간의 곱이라는 걸 식으로 확인했으니 위의 <힘-시간 그래프>에서는 기울기 아래 면적이 충격량임을 눈치챌 수 있다.
진공 상태에서 질량이 같은 자유 낙하한 두 달걀이 지면에 도달하여 정지하는 상황을 보자.
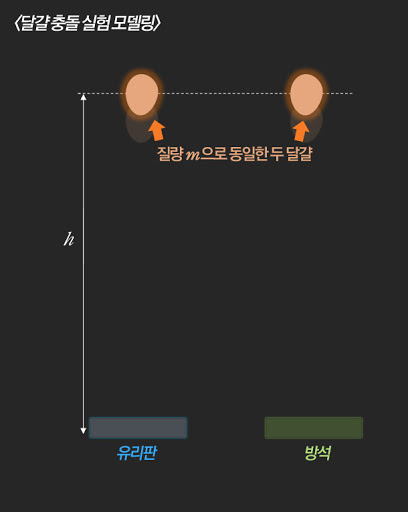
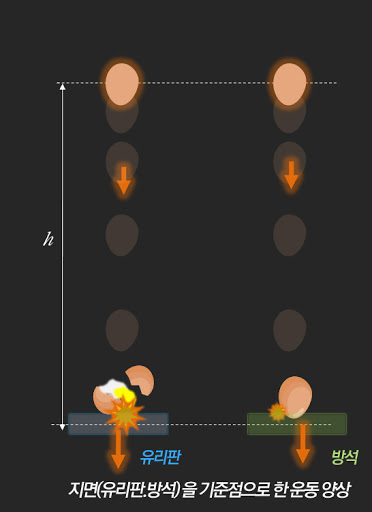
질량이 같은 두 달걀에게 동일한 중력이 작용하기 때문에 두 달걀의 가속도는 같다. 그리고 같은 거리를 이동하기 때문에 유리판과 방석에 같은 속력으로 동시에 도달한다.

낙하한 달걀은 최종적으로 방석과 유리판에 정지하게 된다.
이제 유리판에 떨어진 달걀은 깨지고 방석에 떨어진 달걀은 깨지지 않는 이유를 확인해볼 것이다.
*드래그하면 답 나옴*
지면과 충돌하기 전 달걀의 운동량 = 둘 다 mv
충돌하고 난 뒤 달걀의 운동량= 둘 다 0
달걀의 운동량 변화량의 크기= 둘 다 mv
두 달걀의 운동량 변화량이 같기 때문에 두 달걀이 받는 충격량은 같다.
그러나 왜 방석에 떨어지는 달걀만 깨지지 않을까?
힘의 정의를 생각해보자. 힘이란 물체의 모양을 변화시키는 원인이다. 더 극적인 모양 변화를 일으키기 위해서는 더 큰 힘이 필요하다.
가장 극적인 변화를 보인 유리판에 떨어진 깨진 달걀엔 그만큼 큰 힘 F가 가해졌다는 걸 의미한다.
그렇다면 왜 유리판이 달걀에 작용하는 힘 F가 방석이 달걀에 작용하는 힘 F보다 클까?

달걀이 방석에 떨어질 때에는 운동량이 변화(mv→0)하는 데 걸리는 시간이 상대적으로 더 길고
유리판의 상황에서는 운동량이 변화(mv→0)하는 데 걸리는 시간이 상대적으로 짧아서 그렇다.
이를 그래프로 나타내면 다음과 같다.

즉 충격량이 같으면 힘을 받는 시간이 길수록 작용하는 힘의 크기는 작아지게 되는 거다.
정말 중요한 거를 마지막으로 마무리한다. 눈치챘는지 모르겠지만 이 달걀 낙하 상황에서 두 개의 시간을 고려했다. 바로 달걀이 낙하한 시간과 달걀이 지면과 충돌한 시간이다.
달걀이 낙하한 시간은 두 달걀에게 있어 동일하지만, 달걀이 지면과 충돌한 시간은 각기 다르다는 걸 꼭 짚고 넘어가자.
다음 수업 미리보기
삶의 편의를 위해 물체에 작용하는 힘과 시간의 관계를 이용하는 방법을 공부했고, 그 방법의 기저에는 두 개 이상의 물체가 상호작용할 때 '뉴턴 운동 3법칙'을 만족하는 두 힘의 관계로 인해 보존되는 물리량이 운동량이라는 사실이 있었다. 그러나 이러한 역학적 상황에서 물체의 또 다른 물리량이 보존된다는 사실을 다음 시간에 알게될 것이고, 이 물리량이 운동 상태를 분석하는데 어떤 의의를 가지는지 확인할 것이다.
4. 기출문제 풀어보기
17년도 6월 모평 물리1 4번/ 정답률 82%

답: 5번
19년도 9월 학평 물리1(고2) 5번/ 정답률 78%

답: 3번
13년도 3월 학평 물리1 2번/ 정답률 68%

답: 4번
19년도 6월 학평 물리1(고2) 9번/ 정답률 69%

답: 3번
13년도 4월 학평 물리1 2번/ 정답률 85%

답: 5번
13년도 7월 학평 물리1 2번/ 정답률 76%

답: 3번
16년도 3월 학평 물리1 6번/ 정답률 54%

답: 4번
'2021 물리학I 톺아보기' 카테고리의 다른 글
| 열과 에너지 ① 열역학 1법칙 (0) | 2021.05.11 |
|---|---|
| 일과 에너지(공간으로 바라본 힘) (41) | 2021.04.05 |
| 상호작용하는 두 힘의 관계(뉴턴 운동 3법칙) (0) | 2021.03.20 |
| 힘, 질량, 가속도의 관계를 정리한 뉴턴 (0) | 2021.03.10 |
| 여러 가지 물체의 운동 (0) | 2021.03.04 |



