해당 차시 학습지 파일
성취 기준
물체에 작용하는 알짜힘과 돌림힘이 0일 때 평형을 이룸을 알고, 다양한 구조물의 안정성을 분석할 수 있다.
물리학 전개도
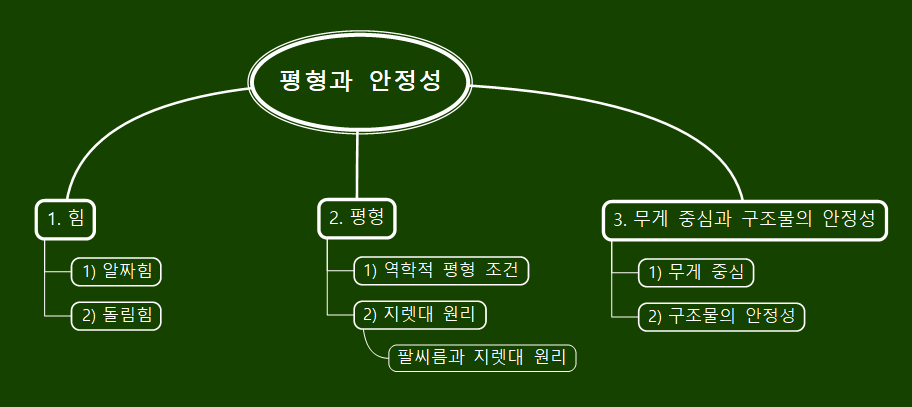
판서 조직도

이탈리아 피사에는 아주 유명한 건축물이 있습니다. 바로 기울어진 탑, 피사의 사탑입니다. 수백 년이 지난 지금도 여전히 기울어져 있지만 놀랍게도 무너지지 않고 버티고 있어요. 피사의 사탑은 단순히 특이한 건축물이 아니라, 물리학의 역사에서 매우 중요한 장소이기도 합니다.
기울어진 곳에서 물리학의 기초를 세우다
17세기 초, 갈릴레이는 이 사탑 위에서 질량이 다른 두 물체를 동시에 떨어뜨리는 실험을 통해 무거운 물체가 더 빨리 떨어진다는 당시의 믿음이 틀렸음을 증명했습니다. 그리고 이 통찰은 후에 뉴턴의 고전역학, 즉 힘과 운동의 법칙으로 이어졌죠. 더불어 피사의 사탑은 한 가지 질문을 던지기도 합니다.
왜 이렇게 기울어져 있는데도 쓰러지지 않을까?
그 답을 알려주는 물리학과 그와 같은 결을 공유하는 삶의 철학을 배우는 시간입니다.
1. 힘
물체에 작용하여 물체의 모양과 운동 상태를 변화시키는 원인
1) 알짜힘(=힘의 합력)
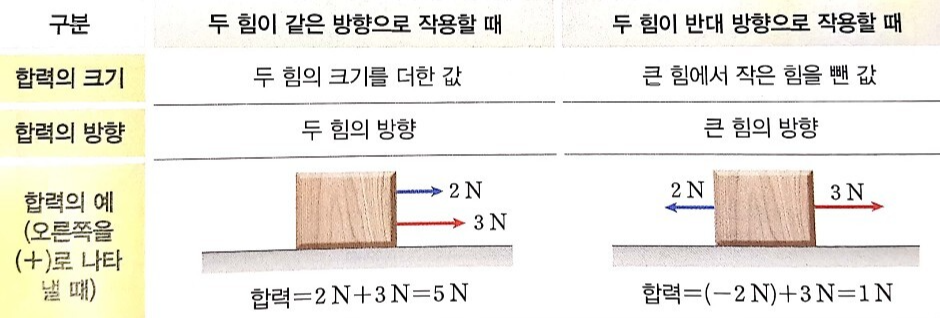
물체에 여러 힘이 동시에 작용할 때 물체는 모든 힘을 합한 하나의 힘이 작용하는 것처럼 움직입니다. 이때 동시에 작용한 여러 힘과 같은 효과를 나타내는 하나의 힘을 알짜힘이라고 해요.
2) 돌림힘(=토크)
① 돌림힘의 크기
우리는 알짜힘이 작용하는 물체는 직선 운동을 한다는 사실을 알고 있습니다. 하지만 주변을 둘러보면, 물체는 단순히 직선으로만 움직이지 않습니다. 문이 열리고 닫히는 움직임, 너트를 조이는 동작, 천체의 공전 운동처럼, 세상에는 회전 운동도 매우 흔하게 일어납니다. 그런데 이러한 회전 운동은 알짜힘만으로는 설명할 수 없습니다. 이 회전 운동의 원인을 바로 돌림힘이라고 합니다.

예를 들어 문을 닫기 위해 회전시킬 때는 큰 힘을 줄수록 문이 더 잘 돌아갑니다. 즉, 돌림힘의 크기는 작용하는 힘의 크기에 비례합니다. 그런데 같은 힘 F으로 문고리를 당기더라도, 회전축(=경첩)에서 멀리 떨어진 곳에서 힘을 주면 문이 더 쉽게 열립니다. 그 이유는, 회전축으로부터 힘이 작용하는 지점까지의 거리 r가 멀수록 돌림힘이 더 크게 작용하기 때문입니다. 이처럼 돌림힘의 크기는 힘의 크기뿐 아니라 작용점과 회전축 사이의 거리에도 비례합니다.
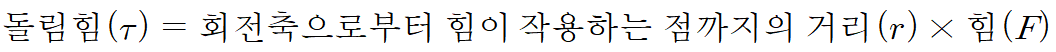
② 돌림힘의 방향

돌림힘의 방향은 오른손 법칙으로 정합니다. 회전하는 방향으로 오른손의 네 손가락을 감쌌을 때 엄지손가락이 가리키는 방향이 돌림힘의 방향입니다. 통상적으로 지면에서 나가는 방향은 +, 지면으로 들어가는 방향은 -로 정합니다.
돌림힘과 일의 단위
돌림힘은 힘과 거리를 곱한 물리량으로, 단위는 N·m인데, 차원만 놓고 보면 힘이 한 일과 똑같습니다. 하지만 힘과 에너지는 명백히 다르죠. 일의 단위는 J임을 상기하세요.
2. 평형
1) 역학적 평형 조건

정지해 있는 물체에 크기가 같은 두 힘이 동일한 작용선상에서 서로 반대 방향으로 작용하면 알짜힘이 0이므로 물체는 계속 정지해 있습니다.

그러나 두 힘이 동일한 작용선상에 있지 않으면, 두 힘의 합력이 0일지라도 돌림힘이 작용하여 물체가 시계 방향(-)으로 회전합니다. 따라서 물체가 운동 상태의 변화 없이 정지해 있는 역학적 평형 상태가 되기 위해서는 다음 두 가지 조건을 동시에 만족해야 해요.
- 힘의 평형: 물체에 작용하는 모든 힘의 합력, 즉 알짜힘이 0이 되어야 한다.
- 돌림힘의 평형: 물체에 작용하는 모든 돌림힘의 합이 0이어야 한다.
2) 지렛대 원리
지레는 힘의 크기를 조절해 주는 도구입니다. 지레를 사용하면 무거운 물체 w를 작은 힘 F만으로도 들어 올릴 수 있어요. 이는 역학적 평형 조건으로 설명할 수 있습니다.
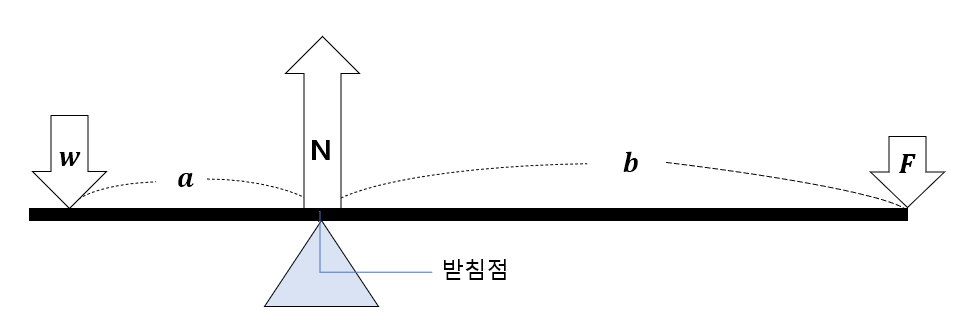
지레가 역학적 평형을 이루기 위해서는 첫 번째 조건인 힘의 평형에 따라 물체의 무게 W와 힘 F의 합이 받침점이 지레를 '떠받치는' 힘(=수직항력) N과 같아야 하며,
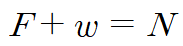
두 번째 조건인 돌림힘의 평형에 따라 물체의 무게 W와 받침점으로부터의 거리 a의 곱이 힘 F과 받침점으로부터의 거리 b의 곱과 같아야 합니다. 그림에서 지렛대의 중심인 받침점이 회전축 역할을 합니다.
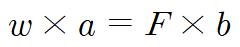

즉, 지렛대의 오른쪽 길이 b가 왼쪽 길이 보다 길수록, 같은 무게라도 더 작은 힘 F으로 물체를 들어 올릴 수 있게 됩니다. 이러한 원리를 바탕으로 아르키메데스는 “나에게 지렛대와 받침점만 주어진다면 지구도 들어 올릴 수 있다”라고 말했어요.
팔씨름과 지렛대 원리

팔씨름 경기에서는 힘이 더 센 사람에게 상대방의 손목을 잡고 시작하도록 하는 핸디캡을 주는 경우가 있습니다. 왜 그럴까요? 이는 지렛대의 원리로 설명할 수 있습니다. 팔씨름을 할 때 팔꿈치는 회전축, 즉 받침점의 역할을 합니다.
① 손목을 잡는 사람
팔꿈치에서 힘 작용점까지의 거리가 짧아 같은 힘으로도 돌림힘(= 힘 × 거리)이 작아져 불리합니다.
② 손을 잡는 사람
팔꿈치에서 힘 작용점까지의 거리가 길어 같은 힘이라도 더 큰 돌림힘을 가할 수 있어 유리합니다.
3. 무게 중심과 구조물의 안정성
1) 무게 중심
무게 중심이란 물체를 이루는 입자들의 전체 무게가 한 곳에 작용한다고 볼 수 있는 점입니다. 물체의 무게 중심을 찾는 법은 간단해요. 돌림힘의 평형 조건이 만족되는 위치가 바로 물체의 무게 중심입니다.
두 물체로 이루어진 계의 무게 중심을 찾아봅시다.
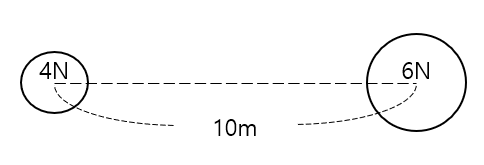
4N의 물체로부터 x만큼 떨어진 위치에 임의의 무게 중심을 정의합니다.

임의의 무게 중심을 회전축으로 설정하여 돌림힘의 평형 조건을 적용합니다.
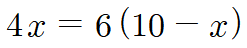

이 계의 무게 중심은 4N의 물체로부터 오른쪽으로 6m 떨어진 지점에 있습니다.
2) 구조물의 안정성
무게 중심은 구조물의 안정성과 밀접한 관계가 있어요.
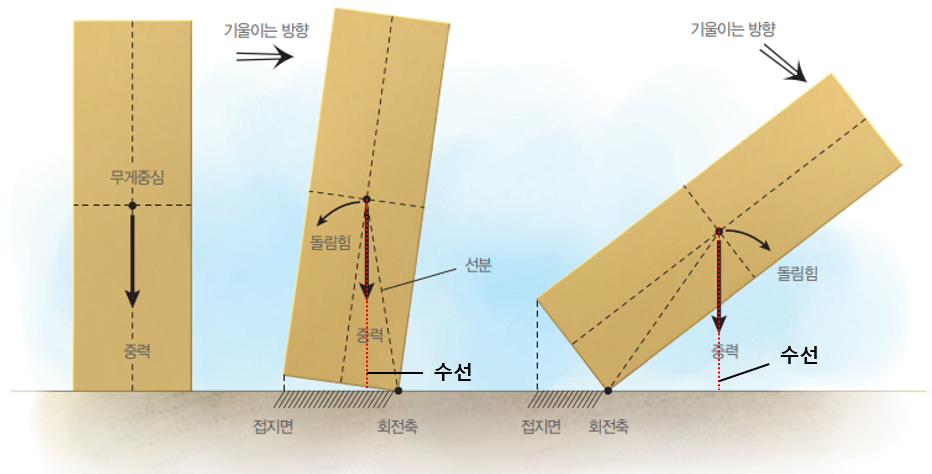
물체가 시계 방향으로 기울어질 때 무게 중심으로부터 수평선에 내린 수선(=빨간 점선)이 회전축을 넘어가지 않으면, 반시계 방향으로 돌림힘이 작용하여 물체는 원래 위치로 되돌아갑니다. 그런데 물체가 더 기울어져 무게 중심에서 내린 수선이 회전축을 넘어가면, 시계 방향으로 돌림힘이 작용하여 물체는 쓰러지게 돼요.

① (가)
만약 이 물체의 무게 중심이 그림처럼 낮은 곳에 위치해 있다면, 수선이 회전축을 넘어가지 않아, 반시계 방향으로 돌림힘이 작용하여 물체는 원래 위치로 되돌아갑니다. 이처럼 물체의 무게 중심은 낮을수록 안정합니다.
② (나)
만약 이 물체의 바닥면이 그림처럼 넓어진다면, 수선이 회전축을 넘어가지 않아, 반시계 방향으로 돌림힘이 작용하여 물체는 원래 위치로 되돌아갑니다. 이처럼 물체의 바닥면이 넓을수록 안정합니다.
On the ground - 로제
https://www.youtube.com/watch?v=i7AUMU-GDNg&list=RDi7AUMU-GDNg&start_radio=1
낮춤으로써 높이 솟아오르다

피사의 사탑이 기울어져도 쓰러지지 않는 이유는, 무게 중심이 아래쪽 낮은 곳에 묵직하게 자리 잡고 있기 때문입니다. 강과 바다가 수많은 골짜기의 물을 받아들이고 다스릴 수 있는 까닭은 그들이 더 낮은 곳에 있기 때문입니다. 나를 낮추는 자세, 겸손은 결코 비굴함이나 자기 비하가 아닙니다. 겸손은 나를 낮춤으로써 오히려 나를 더 큰 그릇으로 만드는 힘입니다.
Everything I need is on the ground
무게 중심이 낮고 바닥이 넓을수록 구조물이 안정되듯, 자신을 낮추는 넓은 그릇을 지닌 사람은 쉽게 흔들리지 않고 삶을 더 단단히 지탱할 수 있습니다. 결국 나 자신에게 절대적으로 필요한 것은 ‘낮은 곳(on the ground)’, 즉 자신의 내면, 겸손의 자리에 있습니다. 로제의 On the ground를 들으며 오늘도 물리를 통해 인생을 배웁니다.
'물리학 이물킥' 카테고리의 다른 글
| 열과 에너지 ① {열의 일당량, 열역학 제1법칙} (2) | 2025.12.19 |
|---|---|
| 역학적 에너지 보존 (1) | 2025.12.05 |
| 뉴턴 운동 법칙 ③ {작용과 반작용의 법칙, 운동량 보존 법칙} (1) | 2025.11.27 |
| 뉴턴 운동 법칙 ② {운동의 표현과 등가속도 운동 공식} (0) | 2025.11.22 |
| 뉴턴 운동 법칙 ① {힘과 운동} (0) | 2025.11.07 |



