
전기 현상은 기원전 700년 무렵 그리스 철학자들로부터 연구되었고, 자기 현상 역시 기원전 2000년 무렵 중국 문헌에 등장했습니다. 19세기에 와서야 별개로 여겨져 왔었던 전기와 자기가 서로 연관 관계에 있다는 사실이 밝혀졌고, 이후 전자기학 이론은 맥스웰의 수학적 이론으로 확립되었어요.
우리는 전자기학의 수혜를 받으며 살고 있습니다. 수많은 전자 기기들은 전자기 유도 현상을 이용한 발전기로 만들어진 전기 에너지를 사용하고, 전기 회로에 의해 제어됩니다. 인간의 감각 역시 신경을 통해 전달되는 전기 신호의 상호 작용입니다. 이처럼 우리 주위 어디에나 전자기학의 원리가 숨어 있습니다.
학습 목표
전기 선속의 개념을 이용하여 가우스 법칙을 유도하고 가우스 법칙의 의미를 설명할 수 있다.
물리학 전개도

판서 조직도
1. 가우스 법칙
점전하가 만드는 전기장은 쿨롱 법칙으로 구할 수 있습니다. 하지만 전하 분포가 만드는 전기장을 쿨롱 법칙으로 구한다면 계산이 복잡해져요. 전하 분포가 만드는 전기장은 대칭성에 기인한 '가우스 법칙'을 이용해 쉽게 구할 수 있습니다.
1) 전기 선속
'선속(flux)'은 '흐른다(flow)'에서 유래한 용어로 전기 선속은 단위 면적을 통과하는 전기력선의 수입니다.
따라서 전기 선속은 면적과 그 면을 통과하는 전기장의 내적입니다.

전기장 또는 가상면의 크기가 방향이 고르지 않더라도 미소 구간에서 전기장이 균일함을 이용하여 전기 선속에 대한 적분식을 나타낼 수 있습니다.

2) 점전하 q가 만드는 전기장
가우스 법칙은 폐곡면(=닫힌 곡면)을 통과하는 전기 선속에 관한 법칙입니다. 점전하 q가 만드는 전기장을 '가우스 법칙'으로 구해볼게요. 점전하 q를 중심으로 반지름이 r인 가상의 구면을 가정합시다. 이렇게 만든 가상의 폐곡면을 '가우스 곡면'이라고 합니다.


가우스 법칙을 해석하면 다음과 같습니다. "가우스 폐곡면 내부의 전하량이 가우스 폐곡면을 지나는 전기 선속을 결정한다." 따라서 가우스 폐곡면 내부에 전하가 없는 경우 가우스 폐곡면을 지나는 전기 선속도 0이 돼요. 균일한 전기장에 놓인 직육면체 가우스 폐곡면을 예로 들어보겠습니다.


이처럼 폐곡면을 지나는 전기 선속은 외부 전기장 유무와 관계없이 폐곡면 내부의 전하만의 영향을 받습니다.
2. 도체와 유전체의 전기장
1) 균일하게 대전된 직선 도선

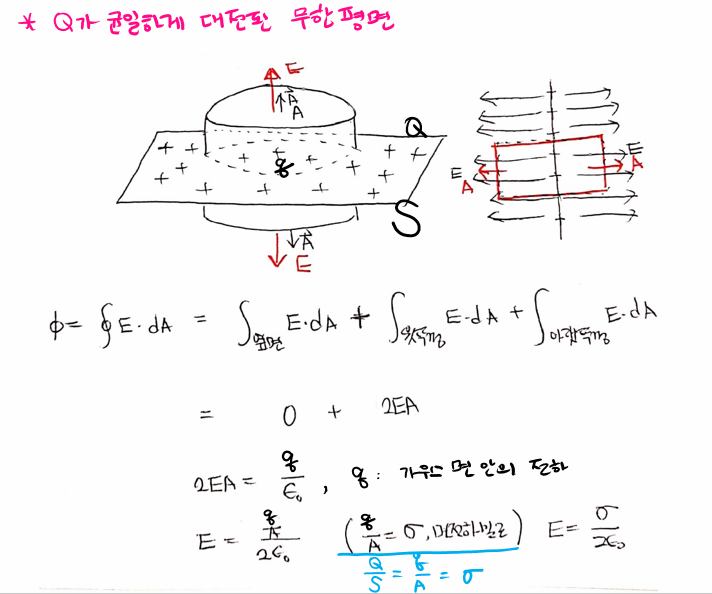
2) 균일하게 대전된 평면
3) 균일하게 Q로 대전된 도체 구 내외의 전기장
도체 내부의 자유 전자는 워낙 자유롭게 움직이다 보니 자유 전자의 알짜 흐름은 0이나 마찬가지입니다. 이는 전자가 전자기적 평형 상태(F=0)에 도달한 것과 같아요. 따라서 도체 내부의 전기장(E=F/q)을 0으로 보아도 무방합니다.
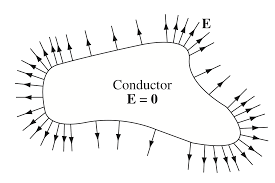
도체 내부의 전기장이 0이므로 도체 내부에 가우스 곡면을 어디로 설정한들 그 가우스면을 지나는 전기 선속은 0이 됩니다.

가우스면을 지나는 전기 선속이 0이라는 건 가우스면 안에 어떤 전하라도 있을 수 없음을 뜻합니다. 따라서 대전된 도체의 전하들은 내부가 아닌 도체 표면에 존재할 수밖에 없습니다.

엘리베이터에서 전화가 잘 안 터지는 이유?
외부 전기장이 있는 공간의 일부를 도체 판으로 둘러싸면 도체 판으로 둘러싸인 내부는 외부 전기장으로부터 영향을 받지 않게 됩니다. 이러한 현상을 '정전기 차폐'라고 해요. 엘리베이터 안에서 데이터가 잘 잡히지 않고 전화가 잘 안 터지는 경우, 전자레인지의 전파가 전자레인지 밖으로 빠져나오지 못하는 경우 모두 정전기 차폐와 관련된 현상입니다.
4) 균일하게 Q로 대전된 유전체 구 내외의 전기장
유전체 구 내부에는 전하가 존재할 수 있습니다. 유전체 구가 균일하게 대전됐다는 건 전하가 유전체 구에 균일하게 분포함을 뜻합니다.

3. 전위
1) 전위의 정의
역제곱 중심력인 만유인력이 보존력이었듯이 역제곱 중심력인 전기력도 보존력이지 않을까요? 이러한 구조적 유사성은 전기력이 보존력임을 암시함과 동시에 전기장에서 정의되는 퍼텐셜 에너지가 있음을 뜻합니다.

전기적 현상은 수많은 전하들이 야기하는 통계적인 결과이기에, 단위 전하가 갖는 값을 기준으로 물리량을 산정하는 것이 효율적입니다. 이런 취지로 단위 전하가 갖는 전기 퍼텐셜 에너지를 '전위'라고 정의합니다. 다시 말해 '전위'란 단위 전하 q의 전기 퍼텐셜 에너지(U)를 단위 전하 q로 나눈 값입니다.
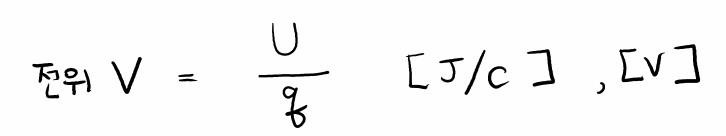
중력 퍼텐셜 에너지가 기준면에 따라 달라지듯이 전위 역시 기준면에 따라 값이 달라집니다. 더불어 두 지점의 '중력 퍼텐셜 에너지의 차이'는 기준에 관계없이 같은 값을 가지듯이 두 지점의 '전위차' 역시 기준에 관계없이 같은 값을 가져요.

2) 점전하 q에 의한 전위

3) 등전위면
같은 전위에 해당되는 지점을 이은 궤적을 '등전위면'이라고 합니다. 이때 전기장의 방향은 등전위면에 수직해요. 중력장의 방향이 중력 퍼텐셜 에너지가 같은 지점을 이은 선과 수직 관계임을 떠올리면 어렵지 않습니다.

4. 전기 쌍극자
크기가 같고 부호가 다른 두 전하를 '전기 쌍극자'라 합니다. 전기 쌍극자는 물 분자와 같은 극성 분자들의 전기적 성질을 표현하는 데 유용해요.

내용 체크 문제

#1번 해설
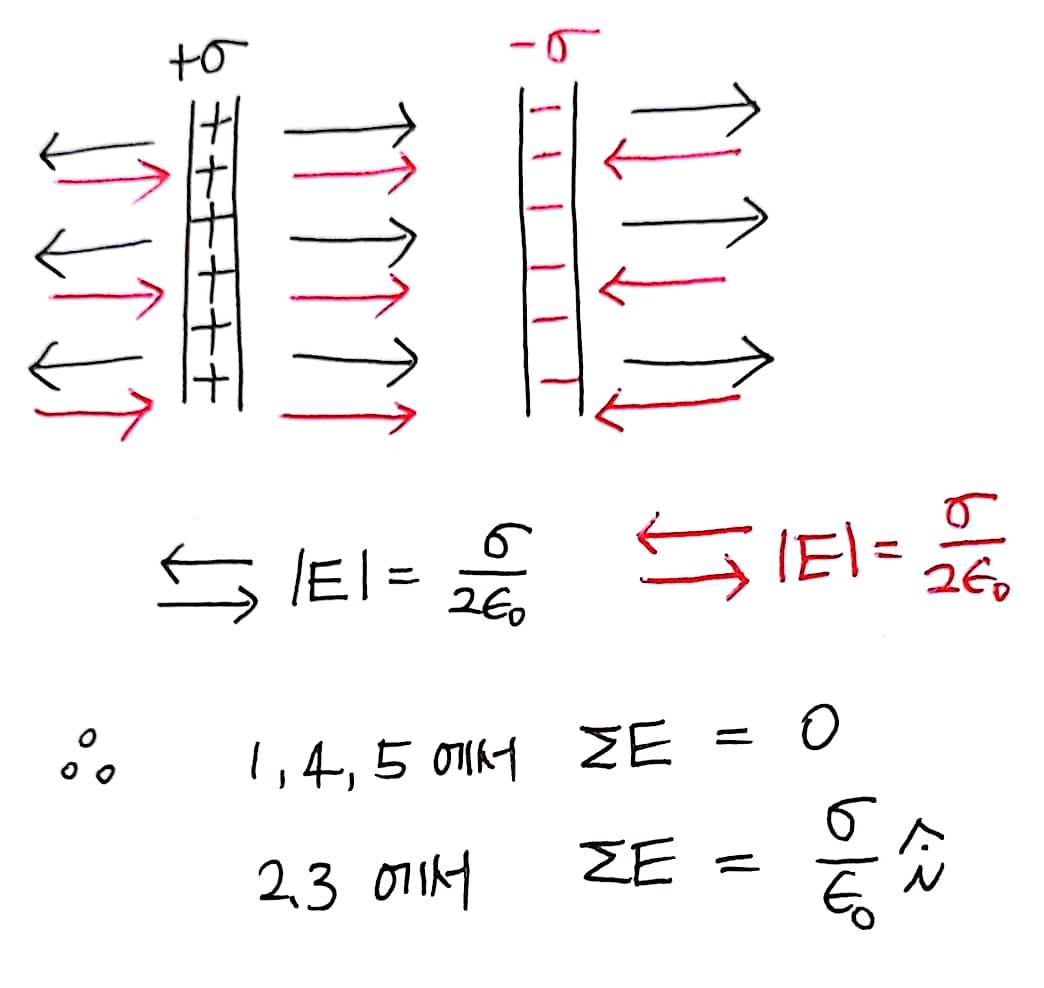

#2번 해설

'2024 고급물리학' 카테고리의 다른 글
| [고급물리학] 키르히호프의 법칙 (2) | 2024.04.22 |
|---|---|
| [고급물리학] 축전기 (3) | 2024.04.16 |
| [고급물리학] 행성의 운동과 케플러 법칙 {만유인력} (1) | 2024.04.11 |
| [고급물리학] 관성모멘트와 돌림힘으로 설명하는 회전 운동 {돌림힘, 관성모멘트, 각운동량} (3) | 2024.04.01 |
| [고급물리학] 입자계의 운동 {운동량 보존 법칙, 운동량과 충격량, 질량 중심} (1) | 2024.03.29 |



