1. 파동은 왜 sin함수의 형태로 표현할까?
파동은 왼쪽 그림처럼 주로 'sin함수' 형태로 표현된다. 한 번은 이런 질문을 해보았을는지 모르겠다. 파동은 하고 많은 함수 중에 왜 sin함수 형태로 표현될까? 그에 대한 답은 오른쪽 그림에 있다.
파동을 수학적으로 기술하기 위해 만든 '파동 방정식'의 해가 'sin함수'이기 때문이다.
물결파든 지진파든 줄 파동이든 모든 파동은 '파동 방정식'을 만족하는 'sin함수' 형태를 해로 가지고 있다.
2. 파동의 중첩과 독립성
파동 방정식의 해가 'sin함수'이기 때문에 파동은 입자가 갖지 못하는 고유한 성질 두 가지(중첩과 독립성)를 가지고 있다.
입자와 파동, 각각 서로 만났을 때 일어나는 일?
| 입자의 충돌 | 파동의 중첩 |
| 두 야구공이 서로 충돌하면, 충돌 후 각 야구공의 속력과 운동 방향이 바뀌거나 에너지가 변한다. | 두 파동이 한 지점에서 만나면 서로 겹쳐 있는 동안은 파형이 변하지만, 떨어진 후에는 다시 원래의 파형이 되어 진행한다. |
파동은 중첩되지만 철저히 독립적이다.
두 파동이 한 지점에서 겹칠 때 그 지점에서 매질의 변위(y)는 그 점을 지나는 각각의 파동의 변위(y1, y2)의 합과 같다. 파동이 중첩된다고 해서 원래 파동이 갖던 각각의 파장과 주기가 변하지 않기 때문에 각 파동은 자기의 속력을 유지한 채 서로를 지나쳐, 다시 원래의 파형으로 돌아와 가던 길을 간다. 이는 각 파동이 다른 파동에게 영향을 주지 않을 정도로 독립적이기 때문이다.
sin함수가 갖는 고유한 특징이 sin함수로 표현되는 파동의 고유한 성질인 중첩과 독립성을 설명한다. 이러한 독립적인 파동이 서로 중첩을 일으키기 때문에 파동만이 '간섭'이라는 현상을 발생시킨다.
+TMI 파동이 독립적인 이유를 수학적으로 증명
3. 파동의 간섭
파동이 중첩하기 때문에 일어나는 현상을 '간섭'이라 통칭한다. 간섭이란 파동이 중첩될 때 합성파가 원래 파동보다 진폭이 커지거나 작아지는 현상을 뜻한다.
| 보강 간섭 | 상쇄 간섭 |
| 진동수와 파장이 같은 두 파동이 마루와 마루, 골과 골이 만나도록 중첩되어 합성파의 진폭이 커지는 현상 >두 파동이 같은 위상으로 중첩되는 경우 |
진동수와 파장이 같은 두 파동이 마루와 골, 골과 마루가 만나도록 중첩되어 합성파의 진폭이 줄어드는 현상 >두 파동이 반대 위상으로 중첩되는 경우 |
위상이란 진동이나 파동과 같이 주기적으로 반복되는 현상에서 한 주기 내에서 어떤 상태에 있는지를 나타내는 변수이다. 쉽게 말하면 파동이 전파될 때 위상이 같은 두 지점은 매질의 변위와 운동 상태가 동일하다. 즉, 마루와 마루는 위상이 같고, 마루와 골은 위상이 반대이다.
4. 소리의 간섭
파동이라면 간섭을 일으키기 때문에 응당 파동의 일종인 소리도 간섭 현상을 일으키게 된다.
어떤 지점에서 측정하냐에 따라 소리의 크기가 달라지는 걸 확인했다. 소리는 파동이기 때문에 소리가 크게 들리는 곳은 소리가 보강 간섭하는 지점임을, 소리가 작게 들리는 곳은 소리가 상쇄 간섭하는 지점임을 예상할 수 있다.
우리가 알기로는 위상이 동일한 두 파동은 보강 간섭을 일으키고 위상이 다른 두 파동은 상쇄 간섭을 일으킨다. 따라서 두 스피커에서 나오는 각각의 소리가 위상이 동일하다면 보강 간섭만 일으켜야 한다. 하지만 실험에서 볼 수 있듯이 두 개의 스피커에서 나오는 위상이 동일한 소리는 보강 간섭도 하고 상쇄 간섭도 한다.
도대체 그 이유는 무엇일까?
그 이유는 두 점파원으로부터의 경로차(두 파동이 한 지점에서 만날 때까지 거쳐 간 파동 진행 거리의 차)에 따라 보강 간섭과 상쇄 간섭이 일어나기 때문이다.
소음은 소음으로 지운다.
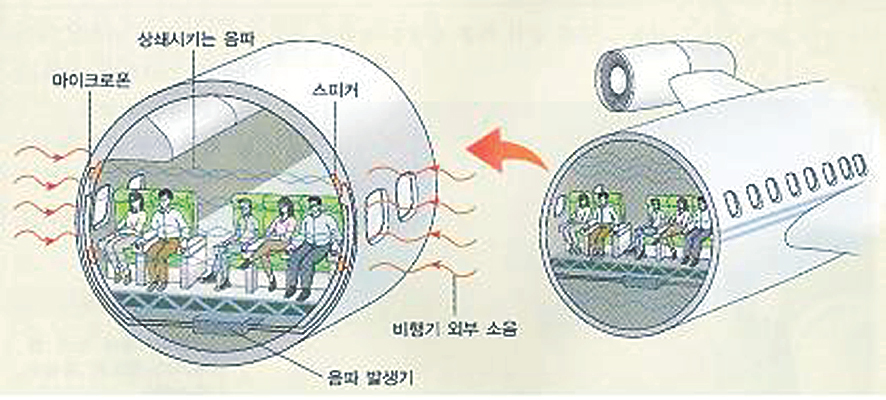
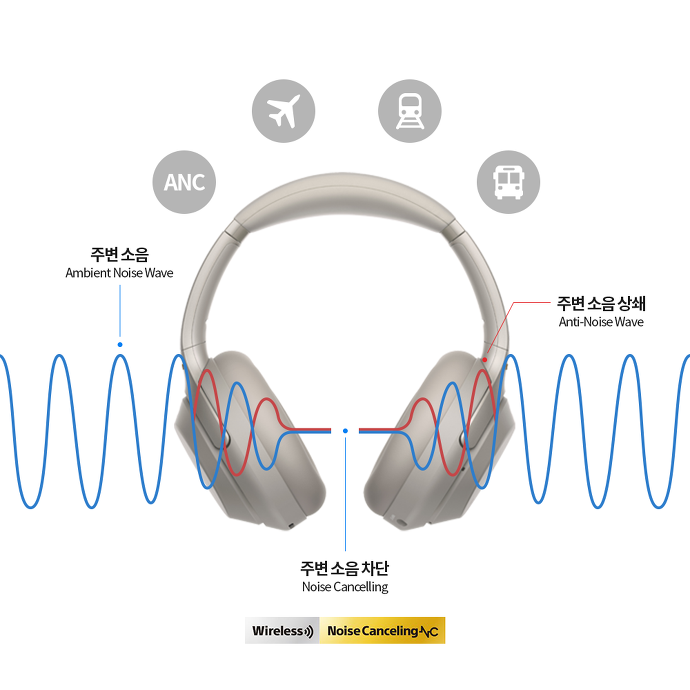
이러한 소리의 간섭 성질을 활용한 '소음 제거 기술' 이외에도 소리의 간섭을 활용한 또 다른 예를 인터넷을 이용해 찾아본 다음 댓글에 달아보자.
'2020 물리학I' 카테고리의 다른 글
| [2015 개정 물리학1] 광전효과 -빛의 입자성- (22) | 2020.12.01 |
|---|---|
| [2015개정 물리학1] 정상파와 빛의 간섭 (40) | 2020.11.17 |
| [2015개정 물리학1] 전자기파의 역사와 전자기파 스펙트럼 (0) | 2020.11.03 |
| [2015개정 물리학1] 전반사와 광통신 (0) | 2020.10.23 |
| [2015 개정 물리학1] 파동의 굴절 (0) | 2020.10.07 |
