2024.03.27 - [2024 고급물리학] - [고급물리학] 힘과 운동 {뉴턴 운동 법칙, 기본 힘, 기타 힘}
[고급물리학] 힘과 운동 {뉴턴 운동 법칙, 기본 힘, 기타 힘}
2024.03.21 - [2024 고급물리학] - [고급물리학] 운동의 표현과 종류 {벡터, 가속도, 포물선 운동, 등속 원운동} [고급물리학] 운동의 표현과 종류 {벡터, 가속도, 포물선 운동, 등속 원운동} 학습 목표
gooseskin.tistory.com
학습 목표
- 일과 운동 에너지와의 관계를 유도하고 그 의미를 설명할 수 있다.
- 퍼텐셜 에너지를 정의하고 퍼텐셜의 수학적 표현 방법을 기술할 수 있다.
- 안정 평형과 불안정 평형을 퍼텐셜 에너지 곡선을 통해 해석할 수 있다.
- 보존력을 정의하고, 보존력의 특성과 예를 설명할 수 있다.
- 역학적 에너지 보존 법칙을 사용하여 물체에 보존력이 작용하는 경우의 운동을 해석할 수 있다.
물리학 전개도

판서 조직도

1. 일-에너지 정리
1) 일과 운동 에너지
① 일


물체에 힘 F가 작용하여 물체가 s만큼 이동했을 때 힘 F는 물체에 F·s만큼의 일을 했다고 정의합니다. 일의 기호는 W(work), 단위는 J
② 운동 에너지

질량이 m이고, 속도 v로 운동하는 물체가 가지는 물리량으로써 기호는 Ek(kinetic energy), 단위는 J
2) 일과 운동 에너지의 관계, 힘에 대한 공간적 접근
 |
 |
① 운동 에너지와 운동량의 차이


운동량과 운동에너지는 운동하는 물체가 갖는 물리량입니다. 이들은 질량과 속도로 표현되는 공통점을 갖죠. 그러나 둘의 태생은 다릅니다. 운동량은 힘과 시간의 관계에서 정의되었고, 운동 에너지는 힘과 이동 거리의 관계에서 정의되었어요.
② 'F=ma'에서 유도하는 일-에너지 정리

2. 다양한 힘이 작용하는 공간에서 일-에너지 정리
1) 중력이 작용하는 공간

2) 탄성력이 작용하는 공간, 용수철

3. 역학적 에너지
1) 퍼텐셜 에너지와 역학적 에너지
 |
 |
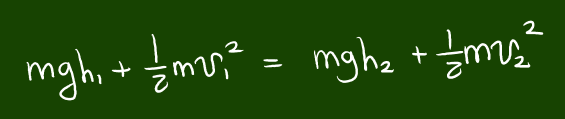 |
 |
'일-에너지' 정리를 통해 중력이 작용하는 공간과 탄성력이 작용하는 공간에서 각 힘이 한 일과 물체의 운동에너지의 관계를 정의했습니다. 결과식의 변수를 이항하여 정리한 식을 살펴보면 특정 위치(x1, x2 or h1, h2)에서 정의되는 무언가의 합이 보존됨을 알 수 있어요. 마치 좌변과 우변의 운동량의 총합이 보존되는 것처럼요.
① 퍼텐셜 에너지
이때 각 변에 운동 에너지가 아닌 항(mgh, 1/2kx^2)을 '퍼텐셜 에너지'라고 합니다.
| 중력 퍼텐셜 에너지 | 탄성 퍼텐셜 에너지 |
 |
 |
중력 퍼텐셜 에너지의 기준면

기준면은 퍼텐셜 에너지가 0이 되는 지점이고, 기준면보다 낮은 위치에서는 퍼텐셜 에너지가 (-) 값을 가집니다.
이때 기준면은 마음대로 정해도 돼요. 대신 처음에 정한 기준면은 일관되게 고수돼야 합니다.
탄성 퍼텐셜 에너지를 구할 때 탄성력이 하는 일만 고려하는 이유

'용수철-물체' 계의 물체에 작용하는 힘은 탄성력 외에도 중력과 수직항력이 있습니다. 그럼에도 '일-에너지 정리'에서 수직 항력과 중력이 한 일이 고려되지 않는 이유는 무엇일까요? 그 이유는 수직항력과 중력의 방향은 물체의 이동 방향과 각각 수직을 이루고 있기 때문에 수직항력과 중력이 한 일의 양이 0이 되기 때문입니다. 정리하면, 이 물체의 운동 에너지 변화에 중력과 수직항력이 기여하는 부분이 전혀 없기에 탄성력이 물체에 한 일만 고려하는 거예요.
② 역학적 에너지
운동 에너지와 퍼텐셜 에너지의 합을 '역학적 에너지'라고 합니다.



오로지 중력과 탄성력만 작용하는, 마찰이나 공기저항을 비롯한 외부 힘이 작용하지 않는 경우에는 역학적 에너지가 보존됩니다.

2) 역학적 에너지가 보존되지 않는 경우
마찰이나 공기저항을 비롯한 외부 힘이 작용하는 경우에 마찰이나 공기저항을 비롯한 외부 힘 f이 한 일만큼 역학적 에너지가 감소합니다.
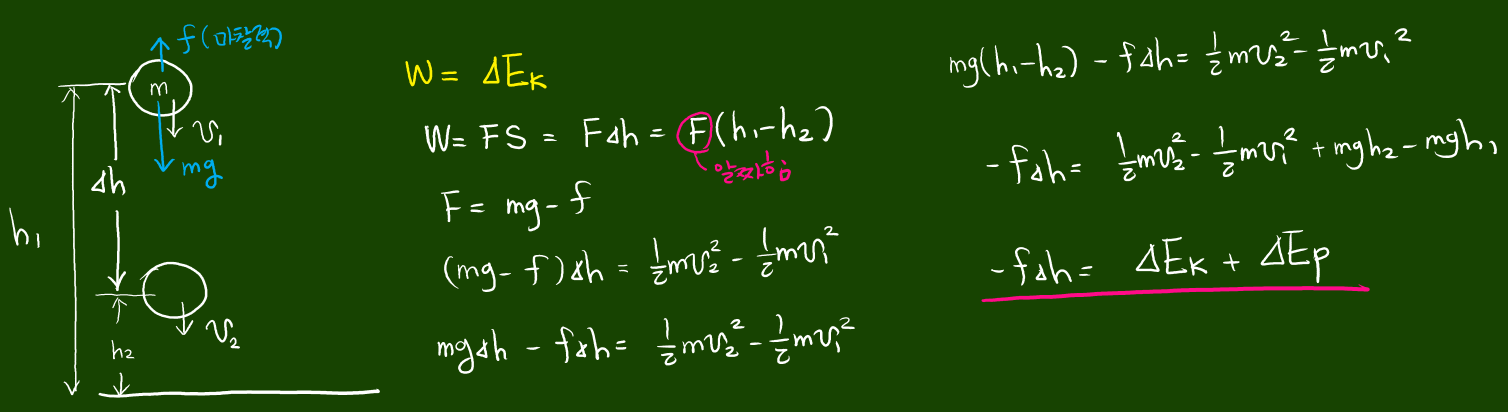
4. 보존력으로 살펴보는 에너지
어떤 힘을 위치에 대해 선적분하는 경우, 처음 위치와 나중 위치가 같으면 어떤 경로를 따라 적분하더라도 그 결과가 같을 때의 힘 f(r)을 '보존력'이라 정의합니다.
1) 보존력의 조건

중력 퍼텐셜 에너지와 탄성 퍼텐셜 에너지의 변화량은 시작점과 끝점이 같다면 이동 경로와 무관하게 크기가 같았습니다. 그 이유는 중력과 탄성력이 보존력이기 때문이죠.
스토크스 정리와 가우스 정리(=발산 정리)의 의의

고등학교 미적분에서는 엄밀히 말하면 스칼라의 미적분만 다룹니다. 그러나 벡터도 미적분할 수 있어요. 스토크스 정리와 가우스 정리는 벡터의 적분법이에요. 이들은 역학과 전자기학에서 굉장히 잘 쓰이는 벡터 적분입니다. 가우스 정리는 3차원을 2차원으로 단순화하는 데, 스토크스 정리는 2차원을 1차원으로 단순화하는 데 의의가 있습니다.
2) 보존력과 퍼텐셜 에너지의 관계

① 중력 퍼텐셜 에너지

중력이 한 일은 오로지 처음과 마지막 위치에만 의존하며 움직이는 경로와는 무관하기에 중력은 보존력입니다.
② 만유인력 퍼텐셜 에너지
이번에는 뉴턴의 만유인력 법칙을 이용하여 만유인력 퍼텐셜 에너지를 다루어봅시다.

③ 탄성 퍼텐셜 에너지

탄성력이 한 일도 오로지 처음과 마지막 위치에만 의존하며 움직이는 경로와는 무관하기에 탄성력도 보존력입니다.
3) 역학적 에너지 보존
역학적 에너지 E는 퍼텐셜 에너지 U와 운동 에너지 K의 합입니다. 보존력만 작용하는 공간에서 계 내부의 물체에 작용하는 보존력이 W의 일을 하면 이 힘은 계의 운동 에너지 K와 퍼텐셜 에너지 U사이에 에너지 변환을 일으킵니다.

비보존력
공기저항을 비롯한 마찰력이 작용하는 계에서는 역학적 에너지가 보존되지 않습니다. 왜냐면 마찰력이 비보존력이기 때문이죠. 이처럼 비보존력이 작용하는 경우 계의 역학적 에너지는 보존되지 않습니다. 이때 역학적 에너지의 변화량은 비보존력이 한 일과 같습니다.

5. 퍼텐셜 에너지로 살펴보는 안정 평형과 불안정 평형
퍼텐셜 에너지 곡선을 분석하여 안정 평형과 불안정 평형의 조건을 구해봅시다.


x2, x3, x4에선 기울기가 0입니다. 따라서 힘이 0이고, 이는 평형 상태에 있다는 걸 의미해요. 그러나 평형이긴 하지만 각 위치의 평형의 종류는 다릅니다. x2, x4에선 입자가 어느 쪽으로든지 변위돼도 입자가 되돌아오게 하는 방향으로 힘이 작용하므로 평형 위치(x2, x4)에서 진동하게 됩니다. 이와 같은 평형 위치를 '안정 평형점'이라고 해요. 반면에 x3에선 입자가 약간이라도 변위되면, 입자는 평형 위치로부터 멀어지는 방향의 힘을 받습니다. 이러한 위치를 '불안정 평형점'이라고 합니다.

수고했어 오늘도 - 옥상달빛
수고했어 오늘도
아무도 너의 슬픔에 관심 없대도
난 늘 응원해, 수고했어 오늘도
완전히 달라진 나를 보여주겠다는 일념으로 하루하루를 애쓰며 수고하는 많은 학생들에게 해주고 싶은 말이 있습니다. 사람 갑자기 변하면 죽는다고 찬물 끼얹는 사람들의 말에 휘둘리지 마세요. '뭐 그렇게 힘들게 올라가려고만 해? 평탄하게 가도 괜찮다'는 말에 넘어가면 힘의 방향과 물체의 이동 방향이 수직인 경우, 힘이 한 일이 0이 되는 것처럼 내가 꿈꾸는 미래의 의미도 유명무실해져 버립니다.
비범한 성공을 얻으려면 비범한 신념을 가져야 합니다. 비범한 사람이 되고자 하는데 왜 비범하지 않은 사람들의 말에 휘둘리려 하죠? 그런 말을 들을 때일수록 내 기준과 가치를 믿으며 나아가야 합니다. 그 고단함을 무릅쓰며 하루하루를 살아내는 나 스스로를 응원하는 사람은 나 자신으로도 충분해요. 아무도 나의 슬픔에 관심이 없대도 '수고했어, 오늘도'라는 말 한마디를 스스로에게 해줄 수 있는 여러분이 되기를 바랍니다. 오늘도 물리를 통해 인생을 배웁니다.
'2024 고급물리학' 카테고리의 다른 글
| [고급물리학] 행성의 운동과 케플러 법칙 {만유인력} (1) | 2024.04.11 |
|---|---|
| [고급물리학] 관성모멘트와 돌림힘으로 설명하는 회전 운동 {돌림힘, 관성모멘트, 각운동량} (3) | 2024.04.01 |
| [고급물리학] 입자계의 운동 {운동량 보존 법칙, 운동량과 충격량, 질량 중심} (1) | 2024.03.29 |
| [고급물리학] 힘과 운동 {뉴턴 운동 법칙, 기본 힘, 기타 힘} (2) | 2024.03.27 |
| [고급물리학] 운동의 표현과 종류 {벡터, 가속도, 포물선 운동, 등속 원운동} (2) | 2024.03.21 |



