물리학Ⅰ 전개도

판서 조직도

목표 기출 문제
19년도 9월 학평 물리1(고2) 1번

답: 4번
22년도 9월 모평 물리학1 1번

답: 1번
1. 운동의 표현
1) 변위와 이동거리

변위와 이동거리는 위치의 변화를 담고 있는 물리량으로 얼핏 보면 같아 보이지만 엄밀히 따지면 다릅니다. '이동거리'란 물체가 실제로 이동한 거리로써 단순히 크기만을 따지지만, '변위 d(displacement)'란 물체의 처음 위치에서 나중 위치까지 잇는 직선 거리로 크기와 방향을 모두 따집니다. 변위와 이동거리 모두 거리와 관련된 물리량이기 때문에 단위는 m입니다.

경로 A, B, C의 이동거리는 모두 다릅니다. 대소를 따지면 C>A>B 입니다. 그러나 A, B, C의 변위는 모두 동일합니다. 크기는 초록선 길이만큼이고, 방향은 북동쪽입니다.
2) 속도와 속력

위 공식의 '이동거리' 자리에 '변위'를 대신 넣으면 '속도 v(velocity)'를 구하는 공식이 됩니다. 크기와 방향을 갖는 '변위'를 시간으로 나눴기 때문에 '속도' 역시 크기와 방향을 갖습니다. 속도와 속력은 시간 대비 거리의 물리량이기 때문에 단위는 m/s입니다.

2초 동안 자동차의 변위는 동쪽으로 22m입니다. 편의상 동쪽을 (+)로 서쪽을 (-)로 정의할게요. 2초 동안 변위가 +22m이므로 자동차의 속도는 +11m/s입니다.
시간-거리 그래프

모름지기 기울기는 y/x로 정의되기에 '시간-거리' 그래프에서는 '기울기 = 속력 or 속도'입니다. 시간-거리 그래프에서는 기울기만이 물리적 의미를 갖습니다.
평균 속도
'평균 속도'란 어떤 특정 구간에서 물체의 운동 속도가 일정치 않을 때, 그 구간에서 물체의 평균적인 속도를 의미하는데요. 물리에서 말하는 평균 속도는 흔히들 평균을 구할 때 사용하는 산술 방식으로 계산하지 않습니다.

평균 속도를 측정하고 싶은 구간의 전체 변위를 통과하는 데 걸린 전체 시간으로 나눠서 구합니다.
3) 가속도
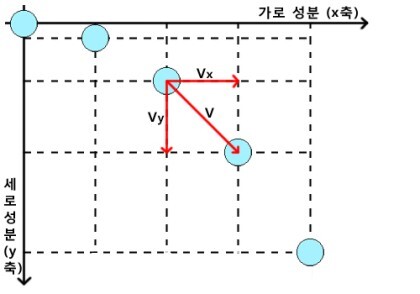
'가속도 a(acceleration)'란 일정 시간 대비 속도 변화를 나타내는 물리량입니다. 따라서 단위는 m/s^2입니다. 가속도도 방향 정보를 갖습니다. 아래 그림에서 물체의 가속도 방향(=속도 변화량 방향)은 (+)입니다.
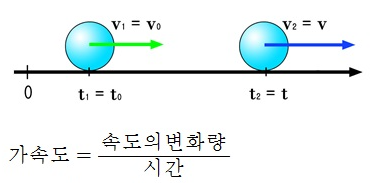



시간-속도 그래프
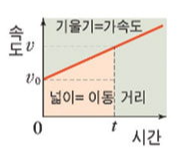
'시간-속도' 그래프에서는 '기울기 = 가속도'입니다. 시간-속도 그래프에서는 기울기 아래 면적 역시 물리적 의미를 갖는데요. 이 그래프의 기울기 아래 면적은 변위입니다. 그 이유는 시간-속도 그래프의 기울기 아래 면적은 속도(m/s)와 시간(s)의 곱으로 정의되는데, 이때 시간(s)이 소거되고 변위(m)만 남기 때문이죠.
2. 운동의 종류
1) 속력과 운동 방향이 모두 일정 - 등속 직선 운동

등속 직선 운동을 그래프로 표현하기
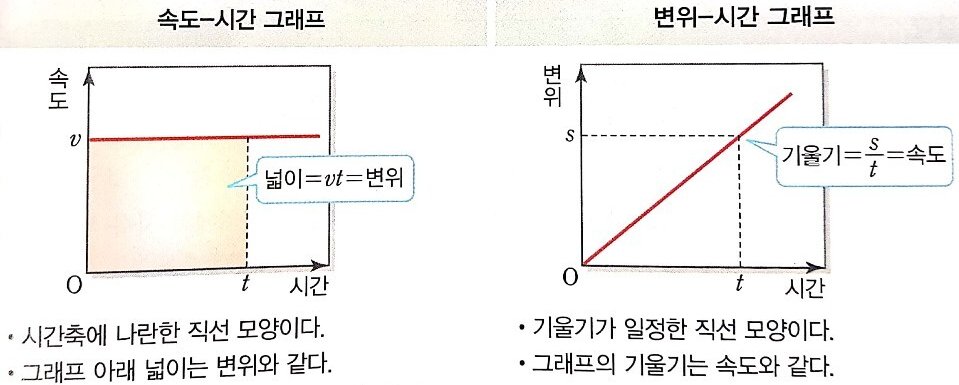
2) 운동 방향만 변함 , 등속 원운동

속도의 크기(=속력)는 일정하겠지만 방향이 계속 변하기 때문에 속도가 일정하지 않은 운동입니다. 따라서 가속도 운동의 한 종류입니다.
3) 속력만 변함, 자유 낙하 운동
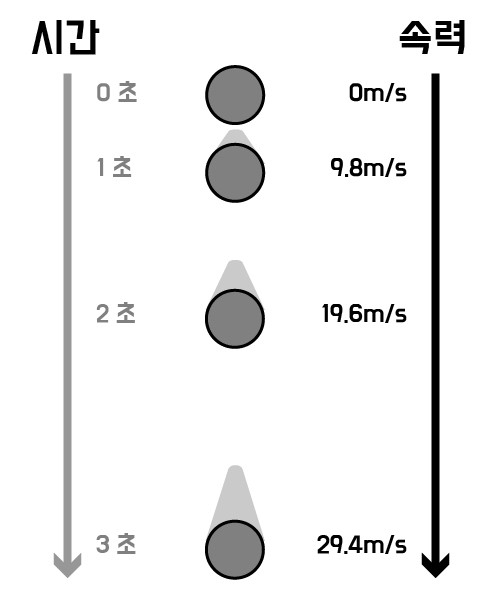
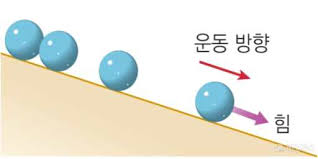
방향이 변하지는 않지만 속도의 크기(=속력)가 계속 변하고 있으므로 속도가 일정하지 않은 운동입니다. 따라서 가속도 운동의 한 종류입니다.
4) 속력과 운동 방향이 모두 변함
ⓛ 진자 운동

② 포물선 운동
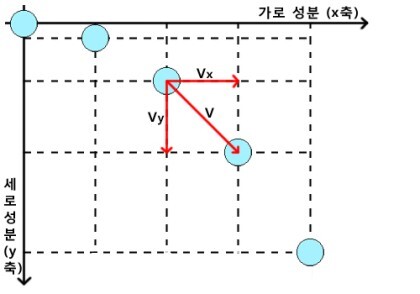
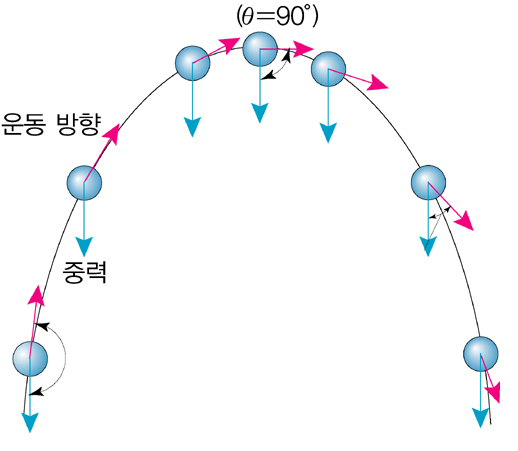
③ 타원 운동
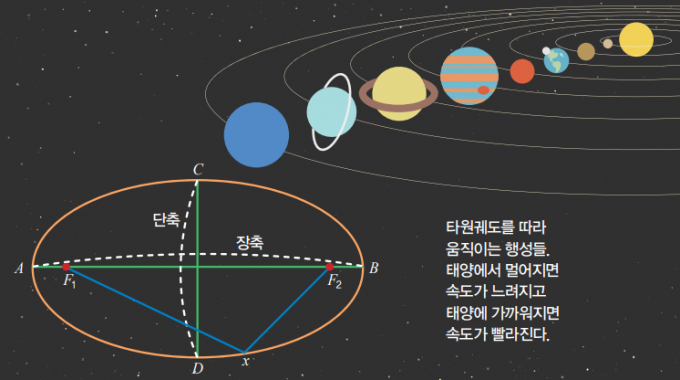
속도의 크기(=속력)와 방향 모두 변하기 때문에 속도가 일정하지 않은 운동입니다. 따라서 가속도 운동의 한 종류입니다.
해와 달 - 조성모
난 이제 가는 길이야. 널 또 못 본 채로
내가 떠나야 올 수 있는 넌데 늘 숨바꼭질하듯 엇갈리잖아.
아마 세상이 끝나기 전에는 늘 이러겠지.
소원이 있어.
차라리 내가 지금 아주 작은 별이라면
슬픈 이별은 하지 않아도 될 텐데
보고 싶은 마음 모아서 너 오면 보라고 노을로 남길게.
해와 달은 천체의 궤도 운동과 슬픈 짝사랑, 서로 완전히 달라 연결이 되지 않는 것처럼 보이는 사실들 사이의 유사함을 가사로 풀어낸 노래입니다. 이러한 창의성이 천상과 지상 사이에 다리를 놓았던 사례들을 알려드릴게요.
기하학으로 천상과 지상을 통합한 뉴턴
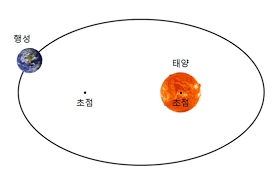
케플러는 태양계 행성들이 타원 궤도를 따라 움직인다는 걸 발견하고, 갈릴레이는 떨어지는 물체가 포물선 궤적을 그리며 움직인다는 걸 발견합니다. 이 각각의 발견들 역시 심오하며 대단하지만 천상의 타원과 지상의 포물선, 전혀 관련이 없어 보이는 두 운동의 기하학적 단일성이 발견됐다는 사실이 더욱 놀랍지 않나요?
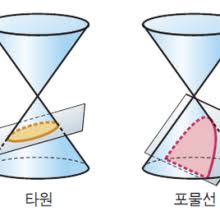
그를 발견한 주인공이 바로 뉴턴입니다. 나무에서 떨어지는 사과와 하늘에서 돌고 도는 달처럼 서로 완전히 달라 연결이 되지 않는 것처럼 보이는 사실들 사이의 유사함을 찾아내는 능력. 바로 여기에서 뉴턴의 천재성이 드러나는 겁니다. 뉴턴은 궤도를 도는 것이 떨어지는 것의 한 형식임을 이해했고, 천상과 지상의 통합을 완성합니다.
제일 처음 굴을 먹은 사람은 누구일까?

조수 간만의 차와 시기는 한 달 내내 급격하게 변해서 어떤 때는 조수 간만의 차가 별로 크지 않지만, 또 어떤 때는 그보다 훨씬 크게 나타납니다. 이처럼 무작위로 나타나는 조류의 패턴은 고대 인류에게 오랫동안 수수께끼로 남았을 거예요. 사실 그들이 조류의 패턴을 쉽게 이해하지 못한 것은 어찌 보면 당연한 일입니다. 왜냐하면, 그에 대한 해답이 누가 봐도 전혀 상관없어 보이는 '밤하늘'에 있기 때문이죠.

즉 최초로 굴을 먹은 사람은 하늘을 주의 깊게 관찰한 고대의 천문학자입니다. 매일 밤 다양한 형태로 밤하늘을 찾아오는, 신비롭게 크고 하얗고 둥근 물체와 바다의 움직임 간의 연결고리를 파악하여 조류를 예측하게 된 그는 언제 바다에 가야 하는지 계획할 수 있었고, 이로써 굴은 안정적으로 구할 수 있는 주식의 한 부분이 될 수 있었죠. 이처럼 창의성은 꾸준한 관심과 지속적인 관찰에서 비롯됩니다. 오늘도 물리를 통해 인생을 배웁니다.
'2024 물리학I 톺아보기' 카테고리의 다른 글
| 운동 방정식 (5) | 2024.03.15 |
|---|---|
| 뉴턴 운동 법칙 ② {운동 3법칙, 힘의 평형} (1) | 2024.03.14 |
| 뉴턴 운동 법칙 ① {운동 1, 2법칙} (1) | 2024.03.12 |
| 등가속도 직선 운동 {평균 속도} (3) | 2024.03.09 |
| 2024 물리학 Ⅰ 프리뷰 (1) | 2024.02.29 |



사이언스토리텔러님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.