2023.10.31 - [2023 물리학I 톺아보기] - 파동의 표현과 성질 ② {굴절}
파동의 표현과 성질 ② {굴절}
2023.10.18 - [2023 물리학I 톺아보기] - 파동의 표현과 성질 ① {그래프 분석, 파장, 주기, 진동수, 속력} 파동의 표현과 성질 ① {그래프 분석, 파장, 주기, 진동수, 속력} 2023.10.13 - [2023 물리학I 톺아보
gooseskin.tistory.com
판서 조직도

목표 기출 문제
22년도 9월 모평 물리학1 4번

답: 4번
21년도 10월 학평 물리학1 6번

답: 3번
3. 파동의 간섭
1) 간섭의 원인, 파동의 중첩과 독립

마주 오는 입자끼리는 충돌하게 되면서 서로의 운동 정보(운동량과 운동 에너지)에 영향을 주기 마련입니다. 하지만 파동의 경우에는 이와 다른 양상을 보입니다.

마주 오는 파동은 충돌하지 않고 중첩돼요. 진폭이 'yA'인 파동 A과 진폭이 'yB'인 파동 B이 만나게 되면 진폭이 'yA + yB'인 파동이 되는데요. 이를 파동의 '중첩'이라 합니다.


파동이 중첩될지라도 서로가 서로에게 영향을 주지 않기 때문에 원래 파동이 갖던 각각의 파장과 주기 그리고 진폭은 변하지 않아요. 따라서 각 파동은 자신의 속력을 유지한 채 다시 원래의 파형으로 돌아와서 각자 가던 길을 갑니다. 이처럼 파동은 독립적이에요. 이러한 파동의 성질, 중첩과 독립이 '간섭'이라는 파동만이 갖는 고유한 현상을 일으키는 원인입니다.
2) 간섭의 종류
'간섭'이란 파동이 중첩돼서 생긴 합성파가 원래 파동보다 진폭이 커지거나 작아지는 현상을 의미합니다. 간섭에는 두 종류가 있어요.
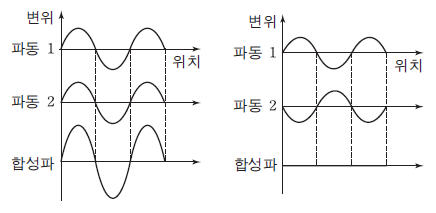
| 보강 간섭 | 상쇄 간섭 |
| 진동수와 파장이 같은 두 파동이 마루와 마루, 골과 골이 만나도록 중첩되어 합성파의 진폭이 커지는 현상 >두 파동이 같은 위상으로 중첩되는 경우 |
진동수와 파장이 같은 두 파동이 마루와 골, 골과 마루가 만나도록 중첩되어 합성파의 진폭이 줄어드는 현상 >두 파동이 반대 위상으로 중첩되는 경우 |
진폭과 위상의 차이
파동에는 '진폭'과 '위상'이라는 물리량이 있는데요. 얼핏 비슷한 개념 같지만 엄밀히 따지면 달라요.
'진폭'이란 진동 중심에서 마루 또는 골까지의 길이, 즉 공간 개념이고요. '위상'이란 진동의 타이밍, 즉 시간 개념입니다.
3) 경로차에 따른 간섭 조건 at 같은 위상의 두 파동
앞서 살펴봤듯이 두 파동의 위상 차이가 간섭의 종류를 결정했습니다. 위상차가 0º인 경우 보강 간섭, 위상차가 180º인 경우 상쇄 간섭이 나타났는데요. 간섭의 종류를 결정하는 또 다른 디테일이 있습니다.
① 수면파의 간섭
두 개의 공을 동일한 박자와 세기로 수면을 쳐줄 때 생기는 수면파들은 위상과 진폭이 같습니다. 따라서 두 수면파는 보강 간섭만 일으켜야 하는데요. 실제로는 보강 간섭과 상쇄 간섭 모두 나타납니다. 왜 그럴까요?

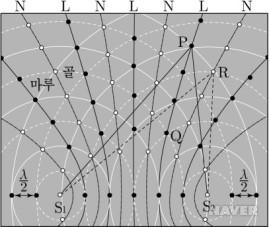
그 이유는 두 파원(=공으로 수면을 쳐주는 곳)으로부터의 경로 차이(=두 수면파가 임의의 지점에서 만날 때까지 이동한 거리의 차이)가 그 지점에서의 파동의 위상 차이를 결정하기 때문입니다.
ⓐ보강 간섭
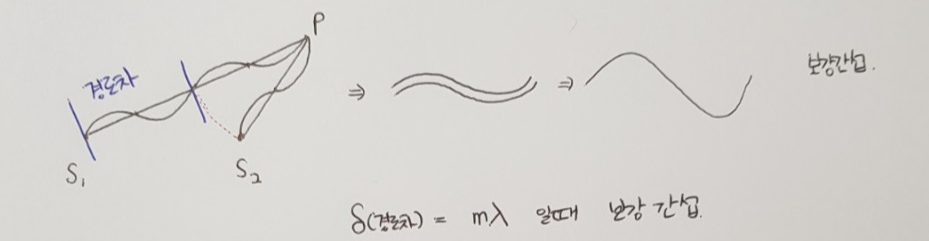
S2에서 p까지 수면파가 한 파장(λ)을 이동할 때, 위상이 같은 또 다른 수면파는 S1에서 p까지 두 파장(2λ)을 이동한다고 가정할게요. 이때 두 파동의 경로가 한 파장(λ)만큼 차이가 나는데요. 이처럼 두 파동의 경로 차이(δ)가 파장의 정수배(=반파장의 짝수배)에 해당되는 지점(p)에선 두 파동이 같은 위상으로 만나기 때문에 보강 간섭이 일어납니다.
ⓑ상쇄 간섭

S2에서 p까지 수면파가 한 파장(λ)을 이동할 때, 위상이 같은 또 다른 수면파는 S1에서 p까지 1.5 파장(1.5λ)을 이동한다고 가정할게요. 이때 두 파동의 경로가 반 파장(λ/2)만큼 차이가 나는데요. 이처럼 두 파동의 경로 차이(δ)가 반파장의 홀수배에 해당되는 지점(p)에선 두 파동이 반대 위상으로 만나기 때문에 상쇄 간섭이 일어납니다.
② 소리의 간섭
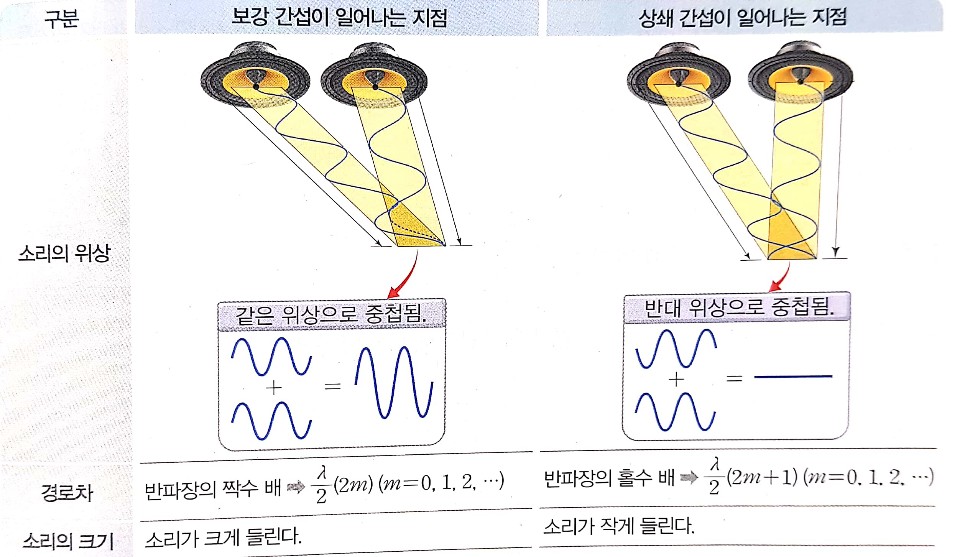
두 파동의 위상이 반대인 경우의 경로차에 따른 간섭 조건
ⓐ보강 간섭
경로차 δ = (2m+1) ½ λ , m=0,1,2.....
ⓑ상쇄 간섭
경로차 δ = (2m) ½ λ , m=0,1,2.....
차수와 간섭 지점의 순서
| 차수 m와 보강 간섭 지점 | 차수 m와 상쇄 간섭 지점 |
| m=0, 중앙 보강 간섭 | m=0, 첫 번째 상쇄 간섭 |
| m=1, 첫 번째 보강 간섭 | m=1, 두 번째 상쇄 간섭 |
| m=2, 두 번째 보강 간섭 | m=2, 세 번째 상쇄 간섭 |
간섭이 나타나는 지점에서 수면파와 소리의 차이
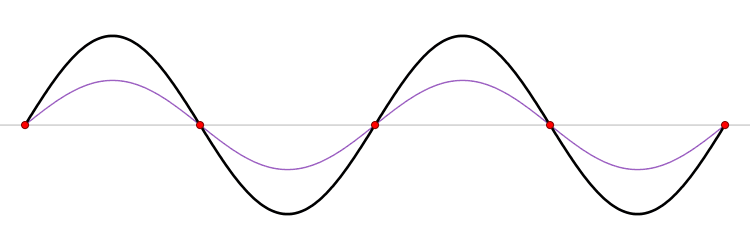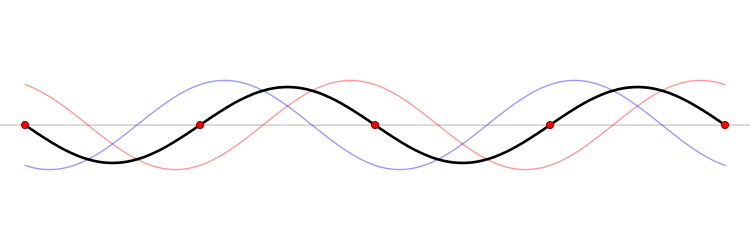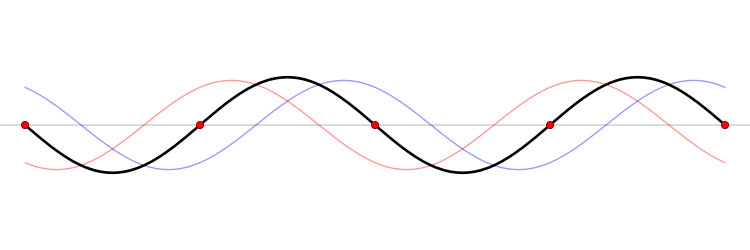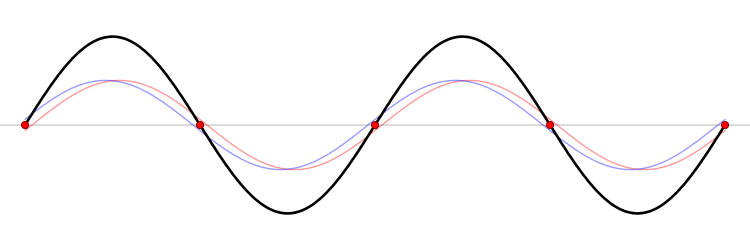
| 보강 간섭하는 지점 | 상쇄 간섭하는 지점 | |
| 수면파 | 최고 수면과 최저 수면이 번갈아 나타남 | 수면의 높이가 변하지 않음 |
| 소리 | 항상 최대 음량 | 항상 최저 음량 |
소리의 음량은 파동의 진폭을 제곱해서 수치화한 값이기 때문에 양의 진폭과 음의 진폭을 분간하는 게 의미 없습니다.
4) 간섭 사례
①보강 간섭
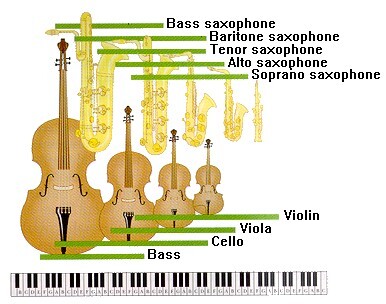
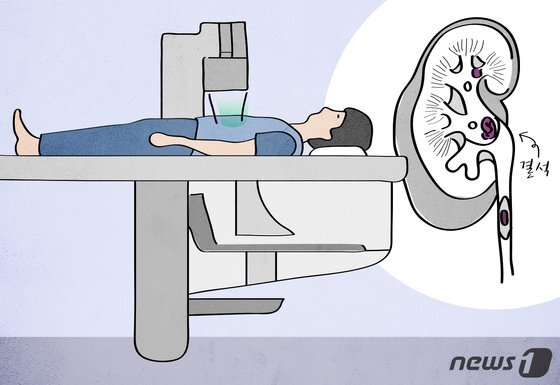

②상쇄 간섭
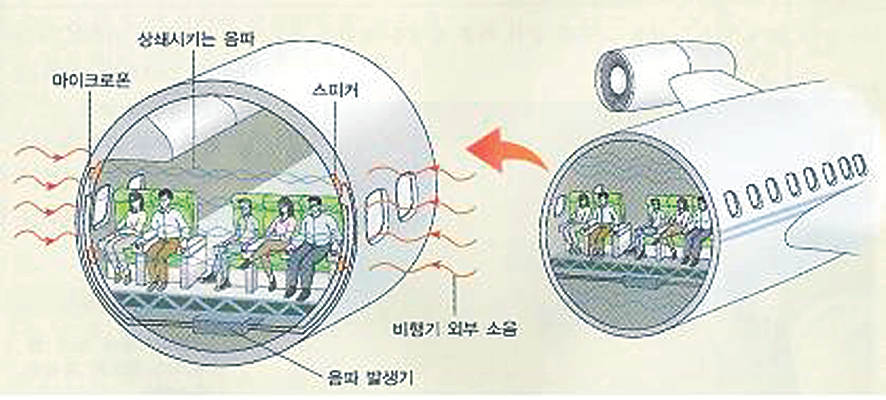
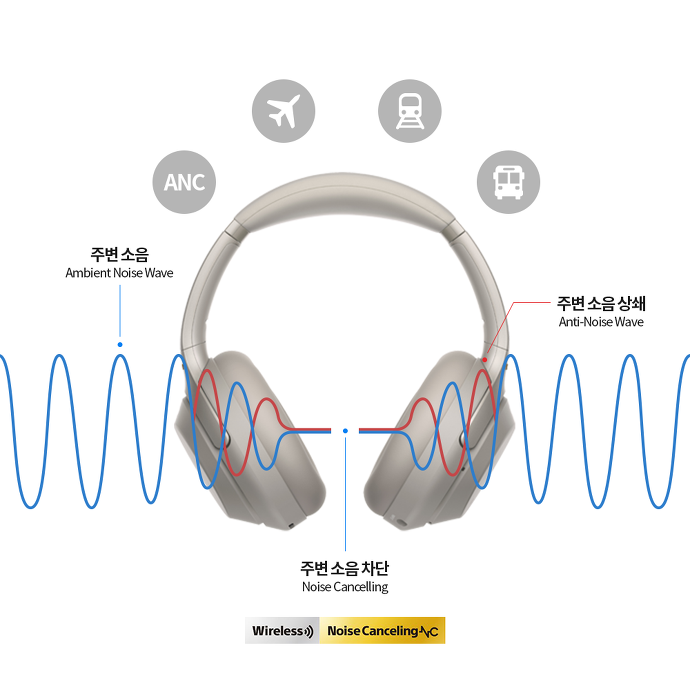
파이팅 해야지 - 부석순
https://www.youtube.com/watch?v=vN0iy88IMLg
2023년이 저물어 가고, 2023년 물리학 I 수업이 끝을 향하고 있습니다. '올해 나만의 수업 정체성을 구축하자'는 저만의 목표 역시 마침표를 향하고 있습니다. 물리학 개념과 삶의 철학을 노래 위에 올려놓고, 그들의 비유적 관계를 살펴보는 것으로 수업을 마무리하는 구성을 매 차시마다 기획해 왔던 게, 어느덧 세 단원만을 남겨두고 있네요.

제가 만든 콘텐츠는 여러분의 파동과 서로 작용하여 간섭 현상을 일으키는 하나의 파동과 같습니다. 이런 간섭 현상으로 여러분 각각이 제 콘텐츠에서 저마다 다른 의미를 발견하길 바랐습니다. 궁극적으로 각자의 교양과 기억, 그리고 독특한 감수성에 맞추어 달리 해석되는 의미들이 주변에 선한 영향력으로 퍼져가기를 바랐죠.
콘텐츠를 기획하고 제작하는 과정에서 겪는 창작의 고통, 뻔뻔하게 프레젠테이션 하는 것 모두 다 쉽지 않습니다. 숱하게 찾아오는 난항 그리고 귀차니즘에 '그냥 이쯤 하고 그만할까'란 생각도 했었지만 '포기는 악덕, 꾸준함은 미덕'이라는 스스로의 철학에 한 점 거짓 없도록 마음을 고쳐 먹고 꾸준하게 해 왔던 과거의 저 스스로가 참 대견스럽네요. 마침표가 느낌표의 한 부분임을 알게 되는 그날까지 파이팅하겠습니다.
도전 기출 문제
22년도 6월 모평 물리학1 15번

답: 2번
2023.11.07 - [2023 물리학I 톺아보기] - 빛의 파동적 성질 ① {스넬의 법칙, 전반사, 광통신}
빛의 파동적 성질 ① {스넬의 법칙, 전반사, 광통신}
2023.11.01 - [2023 물리학I 톺아보기] - 파동의 표현과 성질 ③ {간섭} 파동의 표현과 성질 ③ {간섭} 2023.10.31 - [2023 물리학I 톺아보기] - 파동의 표현과 성질 ② {굴절} 파동의 표현과 성질 ② {굴절} 2023
gooseskin.tistory.com
'2023 물리학I 톺아보기' 카테고리의 다른 글
| 빛의 파동적 성질 ② {빛의 간섭} (0) | 2023.11.08 |
|---|---|
| 빛의 파동적 성질 ① {스넬의 법칙, 전반사, 광통신} (0) | 2023.11.07 |
| 파동의 표현과 성질 ② {굴절} (2) | 2023.10.31 |
| 파동의 표현과 성질 ① {그래프 분석, 파장, 주기, 진동수, 속력} (2) | 2023.10.18 |
| 전자기 유도와 전자기파 ② {전자기파 스펙트럼} (0) | 2023.10.13 |
사이언스토리텔러님의
글이 좋았다면 응원을 보내주세요!
이 글이 도움이 됐다면, 응원 댓글을 써보세요. 블로거에게 지급되는 응원금은 새로운 창작의 큰 힘이 됩니다.
응원 댓글은 만 14세 이상 카카오계정 이용자라면 누구나 편하게 작성, 결제할 수 있습니다.
글 본문, 댓글 목록 등을 통해 응원한 팬과 응원 댓글, 응원금을 강조해 보여줍니다.
응원금은 앱에서는 인앱결제, 웹에서는 카카오페이 및 신용카드로 결제할 수 있습니다.