[고급물리학] 파동의 중첩에 따른 간섭과 회절

2021.05.31 - [2024 고급물리학] - [고급물리학] 변위 전류와 맥스웰 방정식

[고급물리학] 변위 전류와 맥스웰 방정식

 

학습 목표

• 파동의 중첩 현상을 설명할 수 있다.
• 빛의 중첩 현상을 이용하여 초정밀 '정량적' 측정이 가능하다는 것을 설명할 수 있다.
• 회절 현상을 설명할 수 있다.

물리학 전개도

판서 조직도

 

1. 파동의 표현과 성질

이전의 물리학은 질량과 전하, 입자에 대한 역학이었습니다. 입자는 그들이 가지고 있는 물리적 정보(질량, 전하량, 운동량)를 '에너지'라는 그릇에 담아 '힘'을 매개로 전달합니다. 하지만 질량과 형태가 없는 무언가도 자신이 가지고 있는 정보를 '에너지'라는 그릇에 담아 전달할 수 있거든요. 그 무언가가 바로 '파동'입니다. 그렇기에 파동의 역학과 입자의 역학은 상이할 수밖에 없어요. 이 정도면 왜 파동 역학을 공부해야 하는지에 대한 답이 됐을 거라 생각합니다.

 

1) 파동 방정식과 해

(좌) 파동의 표현, (우) 파동 방정식과 해

 

파동을 수학적으로 기술하기 위해 만든 '파동 방정식'의 해는 'sin함수'의 형태를 가집니다. 다시 말해 물결파든 지진파든 줄 파동이든 모든 파동은 '파동 방정식'을 만족하며, 방정식의 해는 'sin함수' 형태를 띠어요.

2) 파동의 중첩과 독립성

마주오는 펄스 각각을 파동으로 취급하겠음

 

마주 오는 입자끼리는 충돌하게 되면서 서로의 운동 정보(운동량과 운동 에너지)에 영향을 주기 마련입니다. 하지만 파동의 경우에는 이와 다른 양상을 보입니다.

 

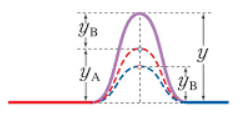
마주 오는 파동은 충돌하지 않고 중첩돼요. 진폭이 'yA'인 파동 A과 진폭이 'yB'인 파동 B이 만나게 되면 진폭이 'yA + yB'인 파동이 되는데요. 이를 파동의 '중첩'이라 합니다. 

 

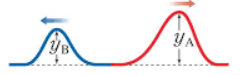
파동이 중첩될지라도 서로가 서로에게 영향을 주지 않기 때문에 원래 파동이 갖던 각각의 파장과 주기 그리고 진폭은 변하지 않아요. 따라서 각 파동은 자신의 속력을 유지한 채 다시 원래의 파형으로 돌아와서 각자 가던 길을 갑니다. 이처럼 파동은 '독립적'이에요. 

 

2. 파동의 간섭

마주 오는 파동은 입자와 달리 충돌하지 않고 '간섭'을 합니다. 그 이유는 파동만이 갖는 고유한 성질, 중첩과 독립성에 있죠.

 

1) 간섭의 종류

'간섭'이란 파동이 중첩돼서 생긴 합성파가 원래 파동보다 진폭이 커지거나 작아지는 현상을 의미합니다. 간섭에는 두 종류가 있어요.

 

(좌)보강 간섭, (우)상쇄 간섭

 

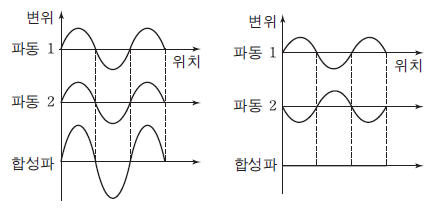
보강 간섭	상쇄 간섭
진동수와 파장이 같은 두 파동이 마루와 마루, 골과 골이 만나도록 중첩되어 합성파의 진폭이 커지는 현상 >두 파동이 같은 위상으로 중첩되는 경우	진동수와 파장이 같은 두 파동이 마루와 골, 골과 마루가 만나도록 중첩되어 합성파의 진폭이 줄어드는 현상 >두 파동이 반대 위상으로 중첩되는 경우

 

진폭과 위상의 차이

파동에는 '진폭'과 '위상'이라는 물리량이 있는데요. 얼핏 비슷한 개념 같지만 엄밀히 따지면 달라요. '진폭'이란 진동 중심에서 마루 또는 골까지의 길이, 즉 공간 개념이고요. '위상'이란 진동의 타이밍, 즉 시간 개념입니다.

 

2) '파동이 독립적인 이유'와 '간섭 조건'의 수학적 증명

 

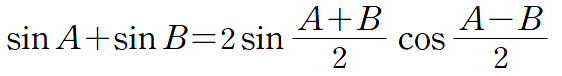
두 파동이 중첩될 때 각 파동의 주기, 파장에 변함이 없는 독립성과 간섭 조건을 수식으로 알아보았다.

하지만 꼭 위상차가 있어야만 간섭 현상이 일어나는 건 아니다. 수면파의 간섭 상황을 살펴보자.

 

3) 경로차에 따른 간섭 조건 at 같은 위상의 두 파동

앞서 살펴봤듯이 두 파동의 위상 차이가 간섭의 종류를 결정했습니다. 위상차가 0º인 경우 보강 간섭, 위상차가 180º인 경우 상쇄 간섭이 나타났는데요. 간섭의 종류를 결정하는 또 다른 디테일이 있습니다.

 

① 수면파의 간섭

두 개의 공을 동일한 박자와 세기로 수면을 쳐줄 때 생기는 수면파들은 위상과 진폭이 같습니다. 따라서 두 수면파는 보강 간섭만 일으켜야 하는데요. 실제로는 보강 간섭과 상쇄 간섭 모두 나타납니다. 왜 그럴까요?

 

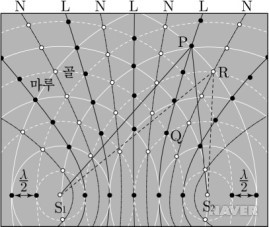
그 이유는 두 파원(=공으로 수면을 쳐주는 곳)으로부터의 경로 차이(=두 수면파가 임의의 지점에서 만날 때까지 이동한 거리의 차이)가 그 지점에서의 파동의 위상 차이를 결정하기 때문입니다.

 

ⓐ보강 간섭

 

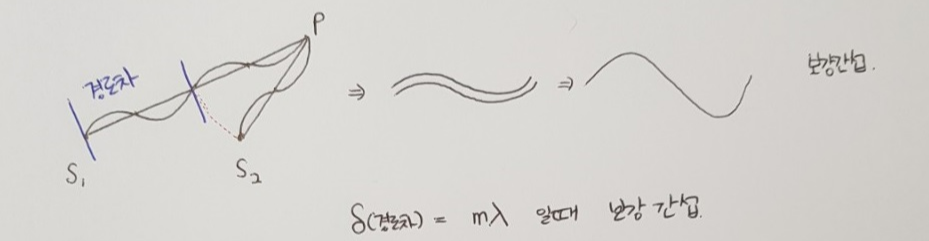
S2에서 p까지 수면파가 한 파장(λ)을 이동할 때, 위상이 같은 또 다른 수면파는 S1에서 p까지 두 파장(2λ)을 이동한다고 가정할게요. 이때 두 파동의 경로가 한 파장(λ)만큼 차이가 나는데요. 이처럼 두 파동의 경로 차이(δ)가 파장의 정수배(=반파장의 짝수배)에 해당되는 지점(p)에선 두 파동이 같은 위상으로 만나기 때문에 보강 간섭이 일어납니다.

 

ⓑ상쇄 간섭

 

S2에서 p까지 수면파가 한 파장(λ)을 이동할 때, 위상이 같은 또 다른 수면파는 S1에서 p까지 1.5 파장(1.5λ)을 이동한다고 가정할게요. 이때 두 파동의 경로가 반 파장(λ/2)만큼 차이가 나는데요. 이처럼 두 파동의 경로 차이(δ)가 반파장의 홀수배에 해당되는 지점(p)에선 두 파동이 반대 위상으로 만나기 때문에 상쇄 간섭이 일어납니다.

 

② 소리의 간섭

 

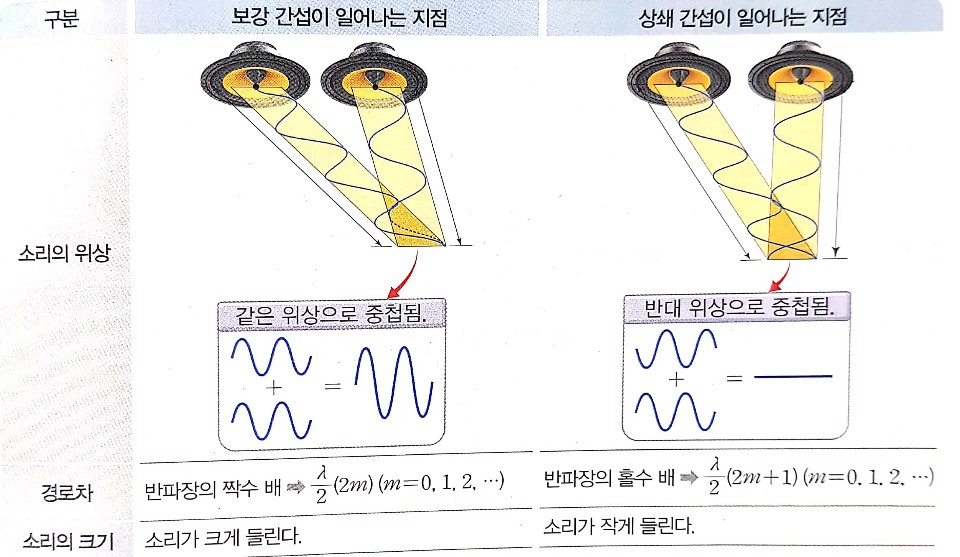
두 파동의 위상이 반대인 경우의 경로차에 따른 간섭 조건

ⓐ보강 간섭

 

경로차 δ = (2m+1) ½ λ , m=0,1,2.....

 

ⓑ상쇄 간섭

 

경로차 δ = (2m) ½ λ , m=0,1,2.....

 

차수와 간섭 지점의 순서

차수 m와   보강 간섭 지점	차수 m와  상쇄 간섭 지점
m=0, 중앙 보강 간섭	m=0, 첫 번째 상쇄 간섭
m=1, 첫 번째 보강 간섭	m=1, 두 번째 상쇄 간섭
m=2, 두 번째 보강 간섭	m=2, 세 번째 상쇄 간섭

 

간섭이 나타나는 지점에서 수면파와 소리의 차이

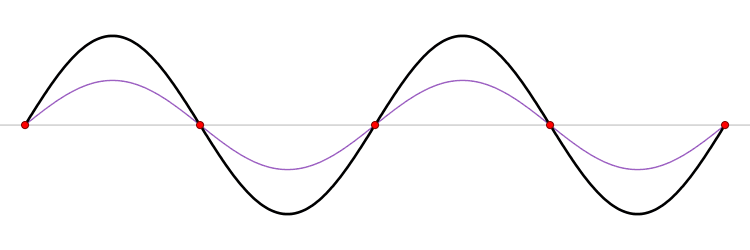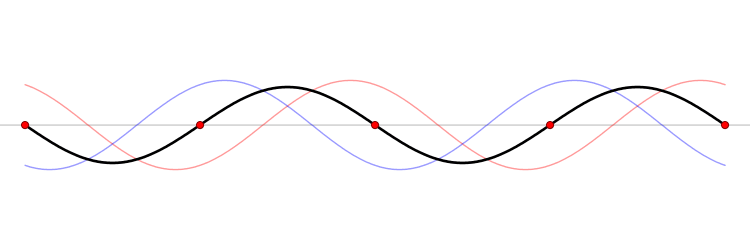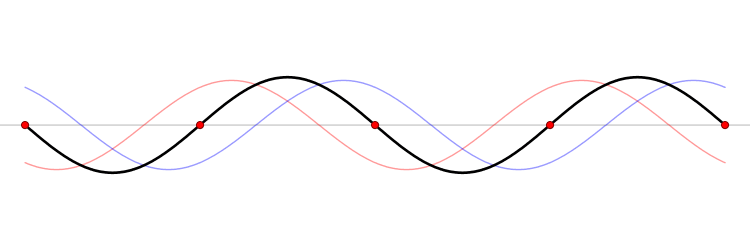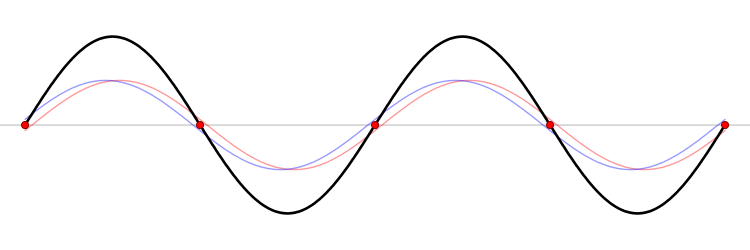
	보강 간섭하는 지점	상쇄 간섭하는 지점
수면파	최고 수면과 최저 수면이 번갈아 나타남	수면의 높이가 변하지 않음
소리	항상 최대 음량	항상 최저 음량

 

소리의 음량은 파동의 진폭을 제곱해서 수치화한 값이기 때문에 양의 진폭과 음의 진폭을 분간하는 게 의미 없습니다.

 

경로차와 위상차의 관계

 

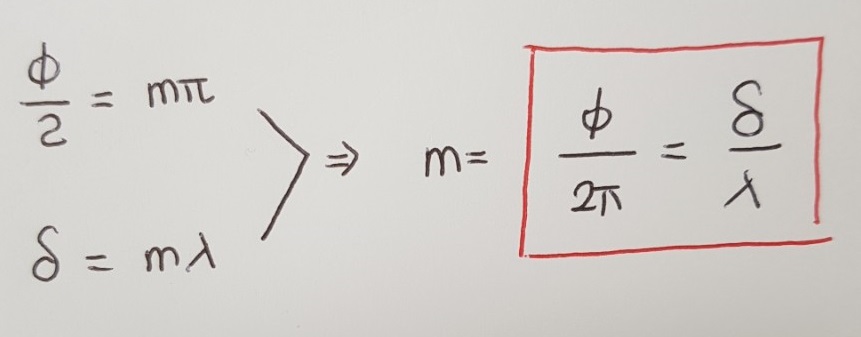
3. 빛의 간섭

 

빛은 파동처럼 퍼져나가기보다는 직진하는 것처럼 보입니다. 그래서 뉴턴은 빛을 입자의 흐름이라고 생각했어요. 이를 토대로 뉴턴의 기하광학은 빛의 반사와 굴절 현상을 설명할 수 있었고, 이를 토대로 렌즈가 등장하게 되었습니다. 이후 렌즈 연구를 통해 망원경을 발명하기에 이르러 천문학의 비약적 발전이 가능했죠. 이때까지는 빛을 입자의 흐름이라고 여기는 뉴턴의 의견에 학계가 힘을 실어주었습니다. 그러나 빛이 파동만이 갖는 간섭과 회절 현상을 보이는 사례들이 속속들이 발견되었어요.

 

1) 이중 슬릿 실험

 

빛이 입자라면 이중 슬릿을 통과하여 직진하기 때문에 스크린에 밝은 띠가 두 군데만 나타나야 합니다. 그러나 영국의 과학자 영은 이중 슬릿을 통과하는 빛이 스크린에 밝고 어두운 여러 개의 띠들을 만든다는 걸 확인해요. 이는 이중 슬릿을 통과한 두 빛이 간섭하고 있음을 의미합니다. 밝은 띠들은 두 빛이 보강 간섭하는 지점이고, 어두운 띠들은 두 빛이 상쇄 간섭하는 지점입니다. 이러한 빛의 간섭 현상은 빛이 파동임을 입증하는 사례예요.

 

경로차로 설명하는 영의 이중슬릿 실험 결과

 

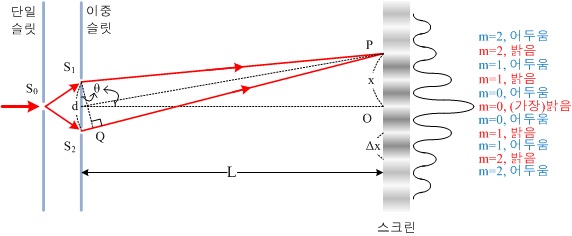
S1과 S2에서 스크린 상의 한 지점(ex: m=2, 2번째 밝은 무늬)까지 두 빛의 이동 경로 차이는 'dsinθ'입니다. θ는 이중 슬릿의 중앙에서 스크린 상의 한 지점(ex: m=2, 2차 밝은 무늬) 사이의 각도입니다.

 

① 중앙에 밝은 무늬가 생기는 이유

S1과 S2에서 스크린의 중앙까지의 거리가 각각 같아서 두 빛의 경로차가 0이 됩니다. 따라서 빛들끼리 보강 간섭을 일으켜요.

 

② 차수 'm'으로 두 빛의 경로차를 찾기

S1과 S2에서 스크린 상의 임의의 지점까지 두 빛의 이동 경로 차는 굉장히 다양합니다. 같은 위상의 두 파동의 이동 경로차가 반파장의 짝수 배인 지점에서는 보강 간섭이 나타나고, 반파장의 홀수 배인 지점에서는 상쇄 간섭이 나타납니다. 

 

 

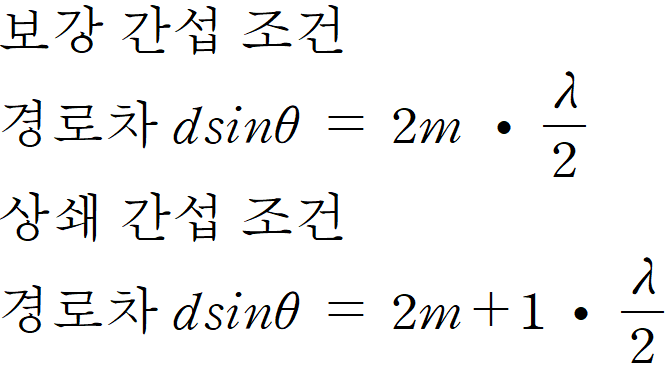
n 번째 밝은(or 어두운)무늬와 차수 m의 관계

밝은 무늬(보강 간섭) 차수 m	어두운 무늬(상쇄 간섭) 차수 m
m=0 (중앙 밝은 무늬)	m=0 (첫 번째 어두운 무늬) - 중앙 밝은 무늬에 바로 이웃함
m=1 (첫 번째 밝은 무늬)	m=1 (두 번째 어두운 무늬)
m=2 (두 번째 밝은 무늬)	m=2 (세 번째 어두운 무늬)

 

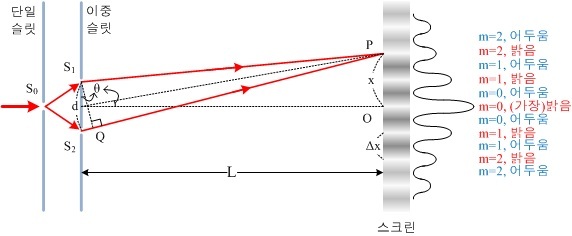
두 번째 밝은 무늬의 차수 m은 2입니다. 따라서 두 빛의 경로차 dsinθ는 '2λ'예요.

첫 번째 어두운 무늬의 차수 m은 0입니다. 따라서 두 빛의 경로차 dsinθ는 '0.5λ'예요.

 

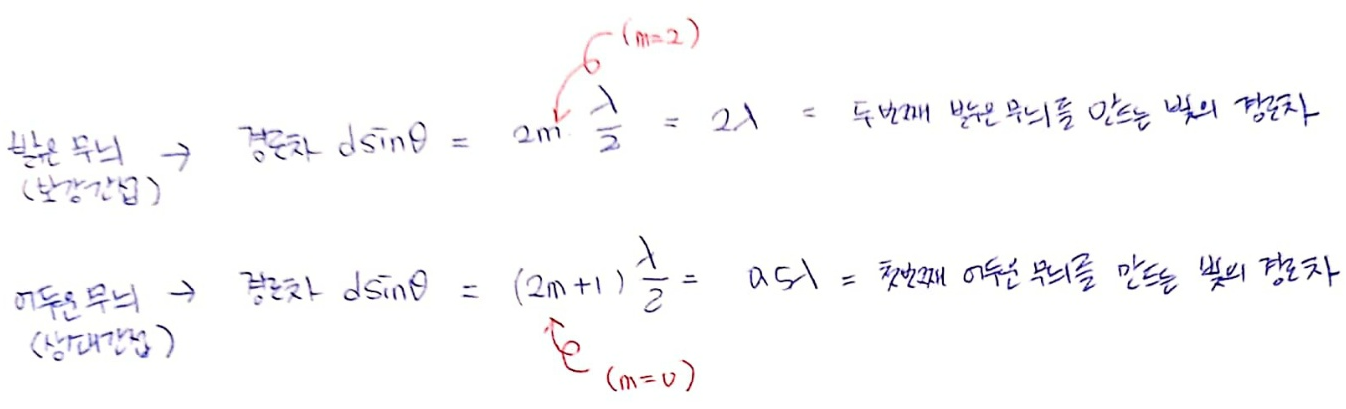
③ 이웃한 무늬 사이의 간격

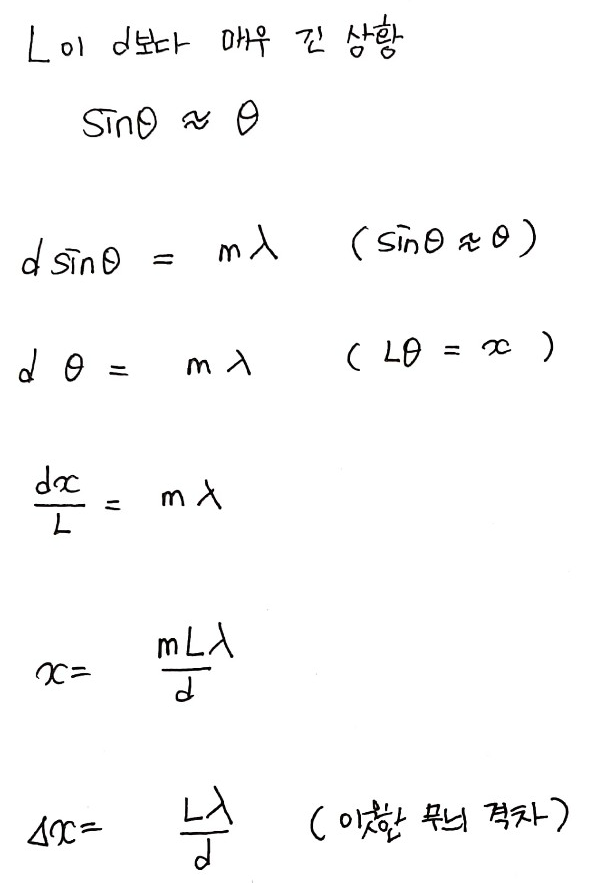
결맞음

영의 이중슬릿 실험 상황을 보면 다음과 같은 의문이 들 수 있어요. "왜 이중 슬릿 앞에 단일 슬릿이 있을까? 그냥 S1, S2에 각각 전구 1개씩 두고 실험하면 안 될까?" 애석하게도 이렇게 실험하면 빛의 간섭 현상은 나타나지 않습니다. 두 빛이 결맞지 않기 때문이죠. 단일 슬릿을 두는 이유는 결맞는 빛을 만들기 위해서입니다. '결맞다'라는 말의 뜻은 무엇일까요?

결맞는 빛과 결맞지 않은 빛

 

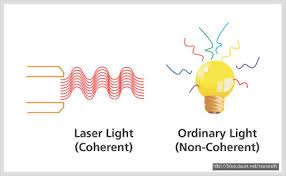
태양, 형광등, 촛불, 백열등을 비롯한 빛들은 열복사 또는 원자 내 전자의 궤도 전이 등등 다양한 광원의 집합체입니다. 다양한 광원에서 방출되는 빛들 각각은 위상이 제멋대로인 데다, 시간에 따른 위상 변화 역시 제멋대로예요. 이런 상태를 '결맞지 않는다'라고 합니다. 결맞지 않는 빛도 빛이기 때문에 간섭을 하지만, 우리 눈은 시간에 따라 불규칙적으로 발생하는 보강 간섭과 상쇄 간섭을 구분하지 못해요. 따라서 S1, S2에 각각 전구 1개씩 두고 실험하면(=두 빛이 결맞지 않아서) 그저 빛 하나에 빛 하나를 더 얹어서 밝기만 밝아지는 결과만 발생할 뿐, 밝고 어두운 규칙적인 띠들은 나타나지 않습니다. 따라서 규칙적인 간섭 띠들을 관찰하기 위해서는 위상차가 시간에 따라 변하지 않는 두 빛으로 실험해야 합니다. 이처럼 위상차가 시간에 따라 변하지 않는 빛을 '결맞는 빛'이라고 해요.

 

2) 렌즈에서의 간섭 현상, 뉴턴링 무늬

(좌) 뉴턴링 무늬 (우) 렌즈의 곡률반경 R 렌즈의 중심에서 어떤 무늬까지의 거리 r 그 무늬지점의 수직거리 d

 

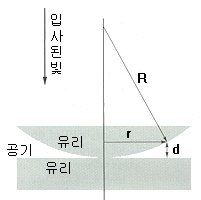
렌즈 제작에 있어 렌즈 곡률 반경을 알아야 하는데요. 렌즈에서의 간섭 현상인 뉴턴링 무늬를 활용하면 렌즈의 곡률 반경을 구할 수 있어요. 뉴턴링 무늬를 이해하려면 '자유단 반사와 고정단 반사' 개념을 알아야 합니다.

 

고정단 반사와 자유단 반사

파동이 진행하는 동안 매질의 종류가 바뀌면 그 경계에서 파동이 반사되고, 일부는 경계를 지나 투과합니다. 이때 소한 매질에서 밀한 매질로 진행하는 파동의 경우, 반사파의 위상은 입사파의 위상과 180도(=반파장)만큼 차이 납니다. 반면에 밀한 매질에서 소한 매질로 진행하는 파동의 경우, 반사파의 위상은 입사파의 위상과 동일해요. 투과파는 어느 경우이든 상관없이 항상 입사파의 위상과 동일합니다.

 

① 중앙에 어두운 무늬가 나타나는 이유

 

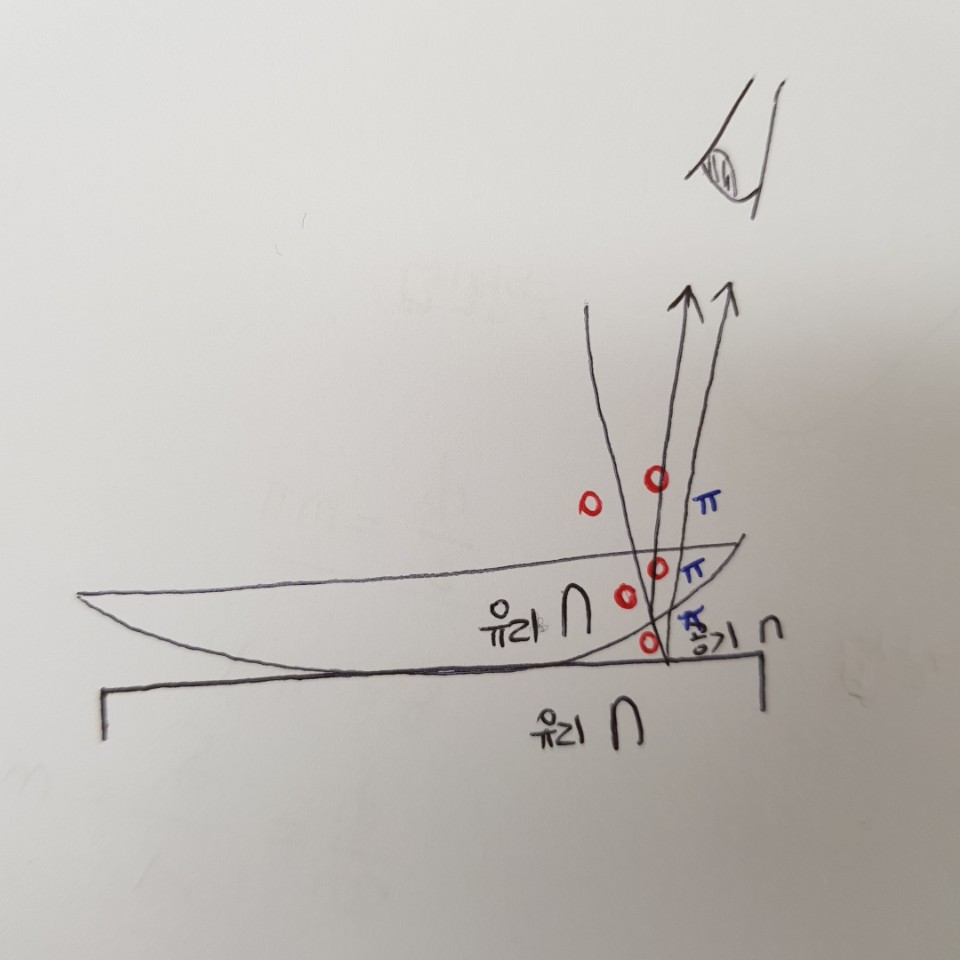
어두운 무늬가 나타나는 지점에서는 두 빛이 상쇄 간섭을 합니다. 렌즈 중심까지 두 빛의 경로차가 0임에도 불구하고 상쇄 간섭이 생기는 이유는 '반사에 따른 위상 변화'로 설명할 수 있어요. 유리의 굴절률이 공기보다 크기 때문에 유리가 밀한 매질, 공기는 소한 매질입니다. 유리에서 공기로 입사하는 빛은 두 빛으로 나뉘는데요. '유리-공기' 경계에서 반사된 빛은 자유단 반사(유리→공기)를 하기 때문에 반사된 빛의 위상은 입사된 빛의 위상과 같아요. 유리를 투과하여 '공기-유리' 경계에서 반사된 빛은 고정단 반사(공기→유리)를 하기 때문에 위상이 180도 변합니다. 따라서 가운데 지점에서는 경로차가 0이어도 눈으로 들어오는 두 빛의 위상차가 180도 차이나기 때문에 두 빛이 상쇄 간섭을 합니다.

 

② 렌즈의 곡률 반경

 

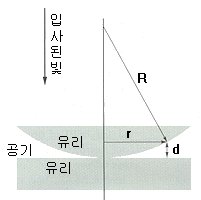
이처럼 빛의 간섭을 활용하여 렌즈의 곡률 반경을 구할 수 있다는 건 빛이 파동이라는 것을 다시 한번 방증하는 셈이에요.

 

4. 파동의 회절

 

보통 입자는 운동 방향에 장애물이 있으면 더 이상 나아가질 못합니다. 반면에 파동은 입자와 달리 장애물에 부딪히면 입자가 갈 수 없는 장애물 뒤쪽까지 이동합니다. 이와 같은 현상을 '회절'이라 해요. 물결파나 음파와 같은 파동은 장애물 뒤쪽까지 전파됩니다. 이처럼 회절은 파동만이 갖는 특성이에요.

 

1) 회절 vs 굴절

파면에 수직한 선은 파동의 진행 경로

 

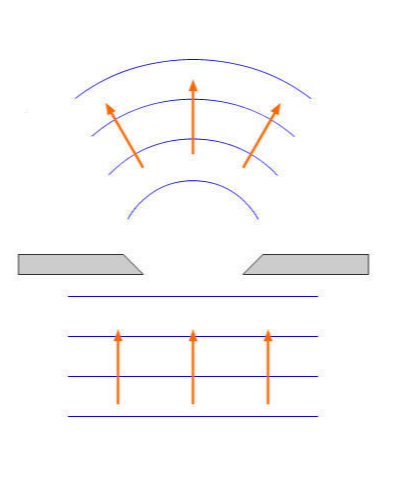
파동은 좁은 틈이나 장애물을 만나면 틈을 통과하여 뒤쪽까지 퍼져 나갑니다. 이러한 현상을 '회절'이라고 해요. 그림을 보면 좁은 틈을 지나 파동이 진행하는 경로가 꺾이고 있는데, 이는 '굴절'을 연상시킵니다. 그러나 '굴절'과 '회절'은 엄연히 다른 물리적 현상이에요.

 

 

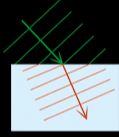
'굴절'이란 파동이 진행하는 속도 차이가 유발하는 물리적 현상입니다. 수면파의 경우, 진행 속도는 수심에 따라 달라져요. 따라서 수심의 변화가 파동의 진행 속도 변화를 유발하고 그에 따라 파동이 굴절돼요.

그러나 장애물 기준으로 수심의 변화가 없음에도 수면파의 진행 방향이 꺾입니다. 이는 하위헌스 원리로 설명할 수 있어요.

 

2) 하위헌스 원리

파동이 전파할 때 각 파면 위의 모든 점은 새로운 점파원이 되어 구면파를 발생시키고 발생된 구면파들의 접면이 새로운 파면이 됩니다. 이를 이용하여 회절 현상을 설명합니다.

 

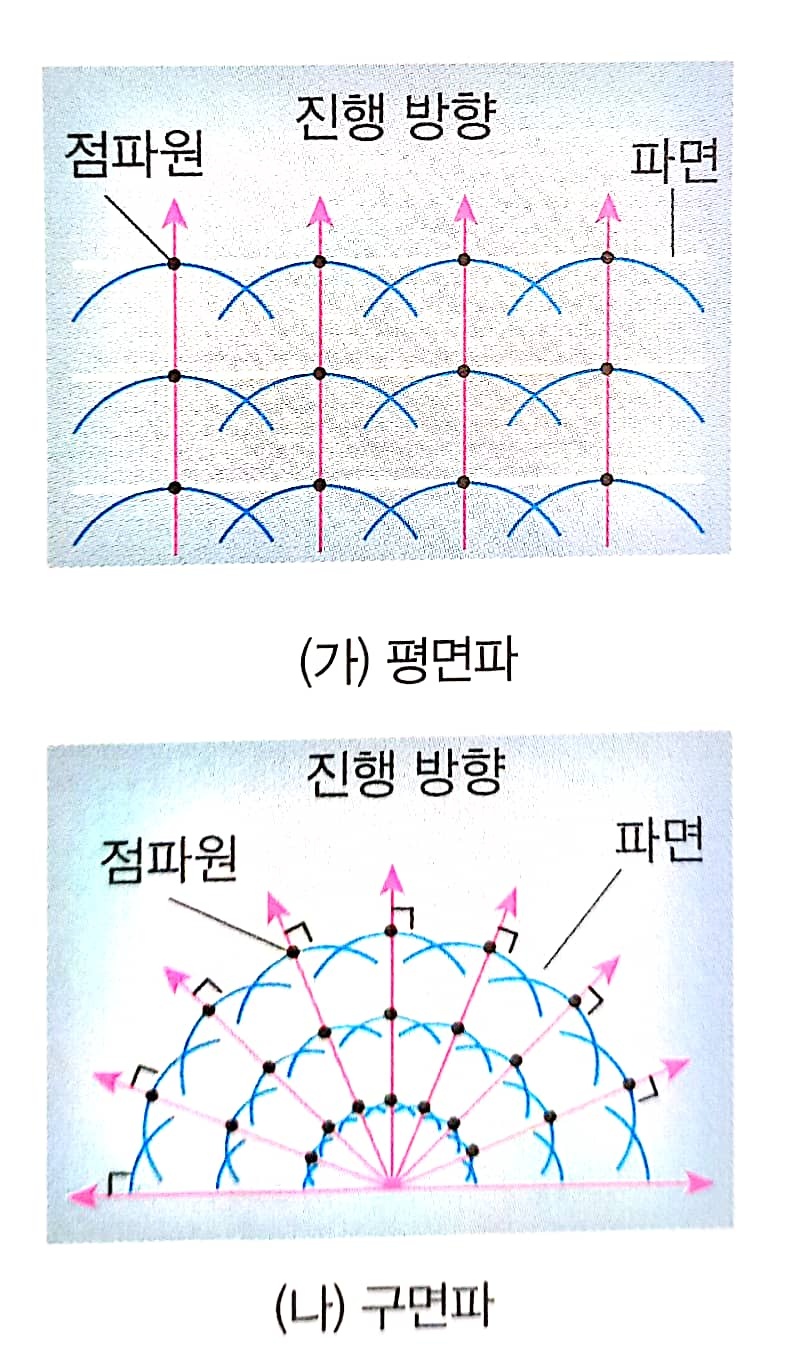
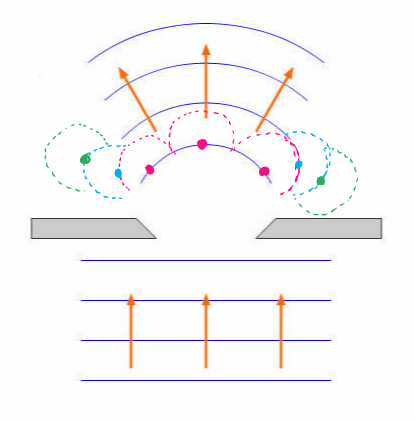
틈을 통과하는 파면 상의 임의 점이 점파원 역할(분홍색 점)을 하고, 분홍색 점파원에서 발생하는 파면 상의 임의 점(파란색 점) 역시 점파원 역할을 하고, 파란색 점파원에서 발생하는 파면 상의 임의 점(초록색 점) 또한 점파원 역할을 합니다. 따라서 전체적으로 틈을 통과한 파동이 주변으로 퍼져 나가는 듯한 형태가 나타나게 돼요. 이를 '회절'이라 합니다.

 

3) 수면파의 회절

 

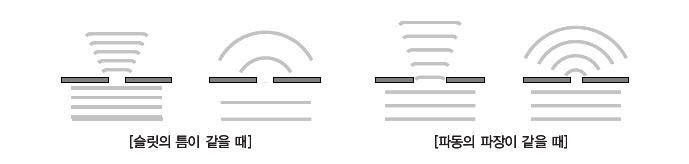
파장이 길고, 슬릿의 폭이 좁을수록 파동의 회절 효과는 더욱 크게 나타납니다.

 

5. 빛의 회절

 

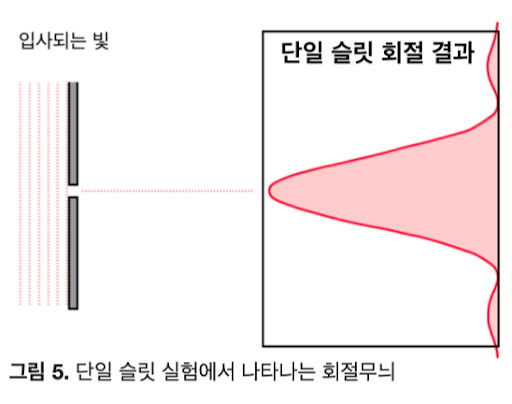
빛이 입자였다면 스크린의 중앙에만 빛이 도달했을 겁니다. 하지만 실제로는 입자였다면 도달할 수 없는 곳까지도 빛이 도달합니다. 이는 빛이 회절하기 때문이에요.

 

1) 회절은 간섭 현상의 일부

 

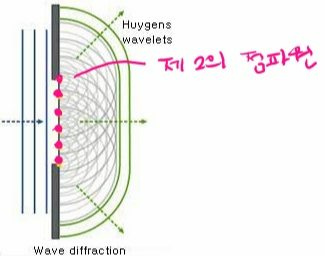
하위헌스 원리에 따르면 슬릿을 통과한 파면 상의 모든 점이 제2의 점파원 역할을 합니다. 따라서 여기에서 발생한 구면파들이 스크린에서 중첩되면서 간섭이 일어나요. 다시 말해 회절이란 파동이 자기 자신과 간섭을 일으키기 때문에 나타나는 현상입니다. 

 

2) 간섭 조건으로 설명하는 회절 무늬

① 중앙 밝은 지점

간격이 a인 단일 슬릿을 통과한 파면 상의 모든 점 각각을 하나의 광원으로 취급할게요. 다음과 같이 슬릿 정중앙의 광원(빨강)을 포함하여 7개의 광원을 가정하겠습니다. 그리고 색별로 광원의 짝을 지어줄게요.(빨강-빨강 짝, 노랑-노랑 짝, 초록-초록 짝)

 

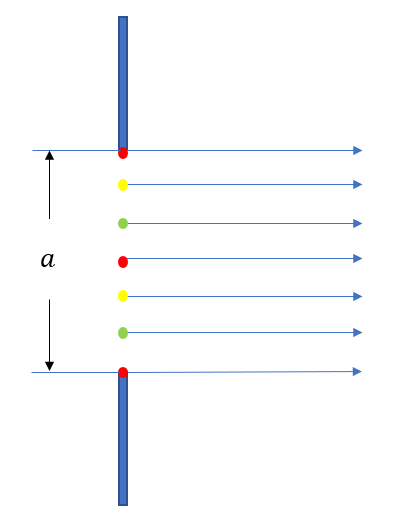
각 광원들로부터 스크린 중앙(P0)까지의 거리가 똑같기 때문에 모든 색깔별 광원들의 경로차가 0이 됩니다. 따라서 중앙에는 밝은 무늬가 생길 수밖에 없어요.

 

 

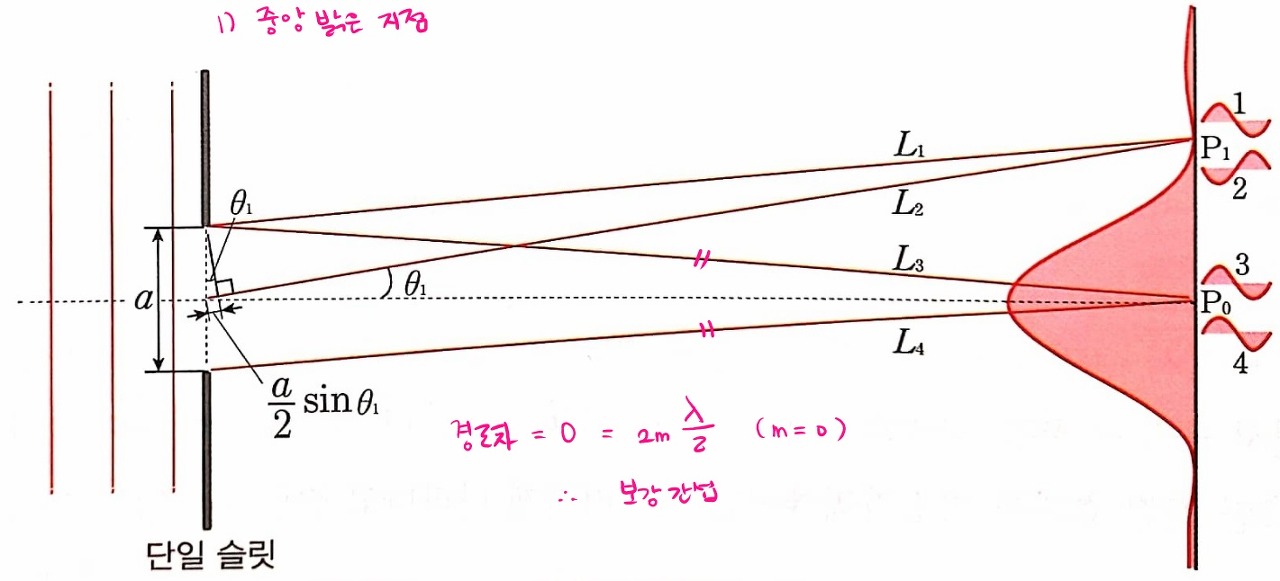
② 첫 번째 어두운 지점

그림에서 θ1는 슬릿의 중앙과 첫 번째 어두운 부분이 나타나는 지점이 이루는 각도예요.

 

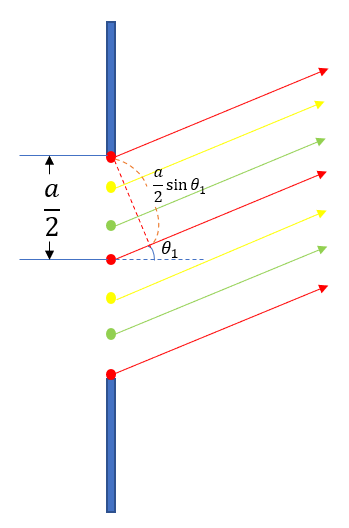
'빨강-빨강' 짝을 이루는 광원에서 첫 번째 어두운 부분이 나타나는 지점까지 두 빛의 이동 경로의 차는 곧 '노랑-노랑' 짝, '초록-초록' 짝과 동일합니다. 결국 색깔별 짝을 이루는 모든 빛들은 P1에서 상쇄 간섭을 하게 돼요.

 

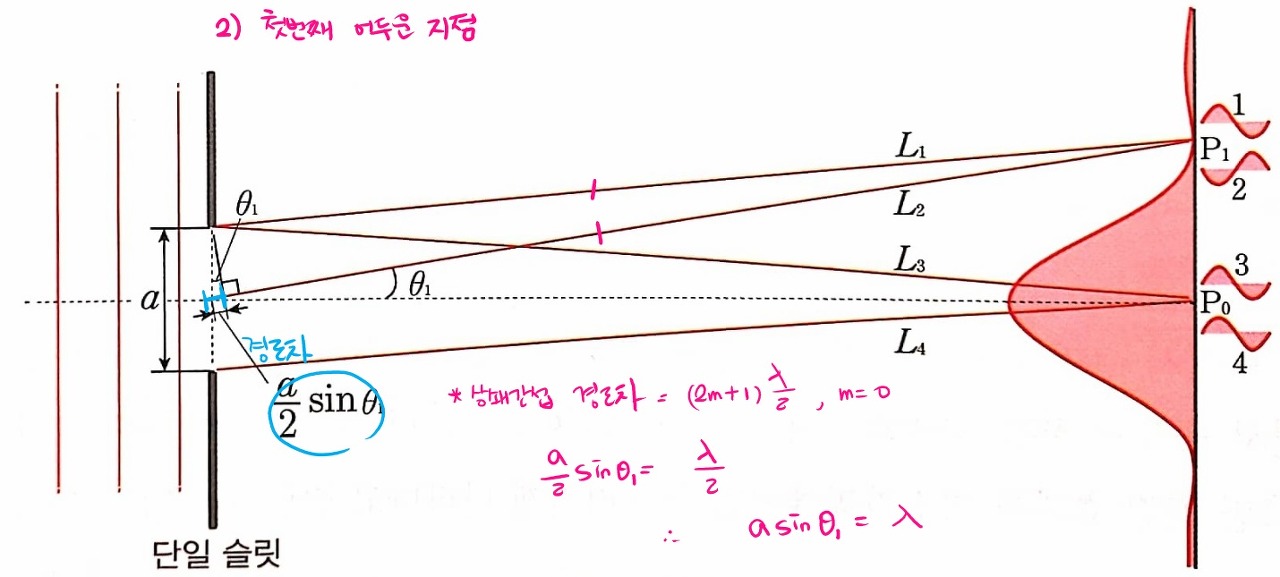
결국 중앙의 밝은 무늬의 폭은 θ1의 크기에 비례하고, θ1의 크기는 파장 λ와 슬릿 폭 a에 의해 결정됩니다. 즉 파장(λ)이 길수록 슬릿의 폭(a)이 좁을수록 중앙의 밝은 무늬의 폭(θ1)은 더 넓어져요. 중앙 밝은 무늬의 폭이 넓어진다는 것은 회절이 잘 일어난다는 말과 같습니다. 따라서 수면파의 경우와 마찬가지로 빛의 파장이 길수록, 통과하는 슬릿의 폭이 넓어질수록 빛의 회절 정도가 커집니다.

 

3) 스크린 중앙에서 멀어질수록 약해지는 무늬의 세기

임의 지점에서 무늬의 밝기를 결정하는 건 그 지점에서 중첩되어 형성된 합성파의 진폭입니다. 무늬의 밝기 I(𝜽)는 진폭 E𝜽의 제곱에 비례합니다. 합성파의 진폭을 구해봅시다.

 

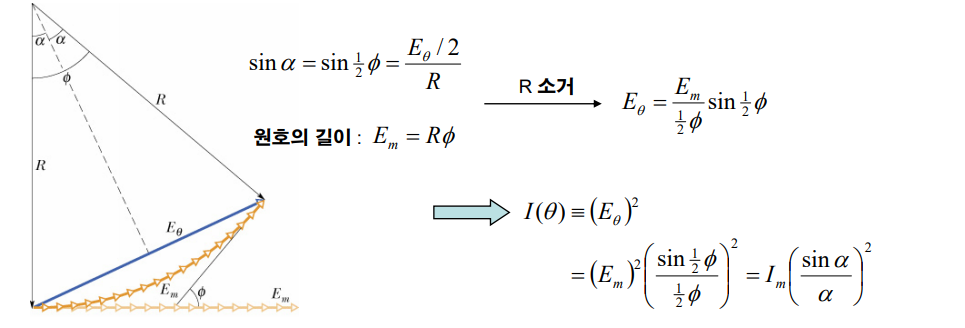
모든 파동의 위상차가 0도라면 합성파 진폭은 Em이 됩니다. 그렇지만 단일 슬릿에서 스크린까지 진행하는 각 파동은 기준 파동에 대해 같은 경로차를 가지게 되니(=같은 위상차를 가지게 되니) 합성파의 진폭이 단순히 Em이 되지는 않고, 그림에서처럼 벡터합을 통해 나온 E𝜽가 됩니다. 이때 그림의 ϕ는 모든 파동의 위상차를 합한 값입니다. E와 전체 위상차 ϕ, Em간의 기하학적 관계를 통해 회절 무늬 밝기와 각도의 관계를 정의할 수 있어요.

 

회절에 의해 나타나는 극소 무늬의 위치

 

m이 0부터 시작되지 않음을 확인하세요. 그 이유는 m이 0인 지점은 경로차가 0인 부분, 즉 중앙 지점인데요.

중앙 지점에는 극소 무늬가 생길 수 없으므로 0을 차수에서 제외합니다.

 

이중슬릿이 만드는 회절 무늬

영의 이중 슬릿 실험을 직접 해보면 이론과는 살짝 다른 패턴이 나타납니다.

 

<이론에 따른 예상 패턴>

 

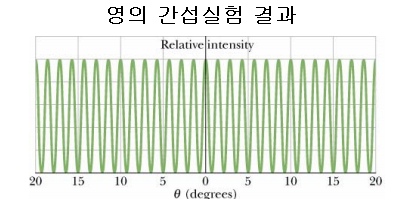
그럴 수밖에 없는 게 이중 슬릿의 개별 단일 슬릿에서 나타나는 회절 현상을 고려하지 않았기 때문이죠.

 

 

 

 

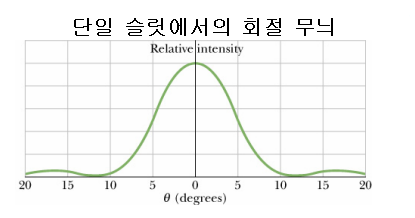
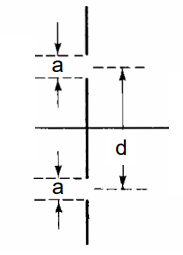
이중 슬릿 간의 간격이 d이고, 각각의 슬릿의 폭이 a이니 

슬릿의 폭이 a인 각각의 슬릿에서의 회절 현상까지 고려해야만 합니다.

실제 무늬의 패턴은 아래와 같아요.

 

 

 

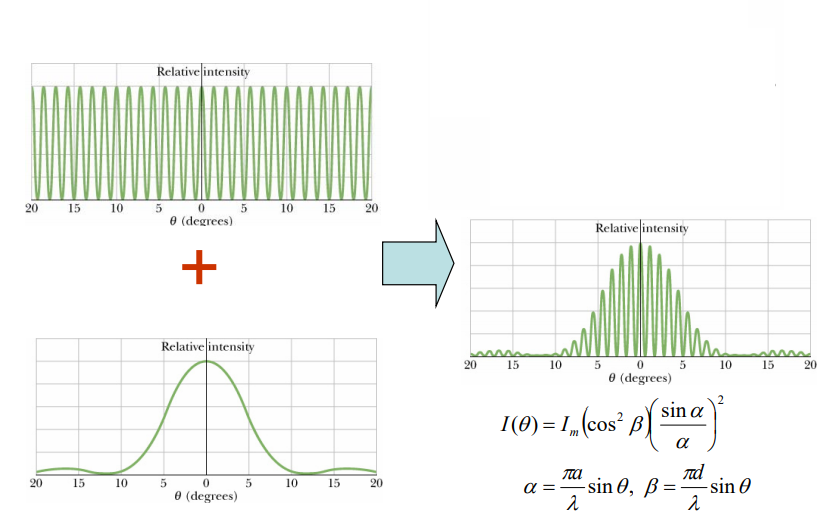
6. 다양한 구조에서의 회절

 

1) 원형 구멍에서의 회절

 

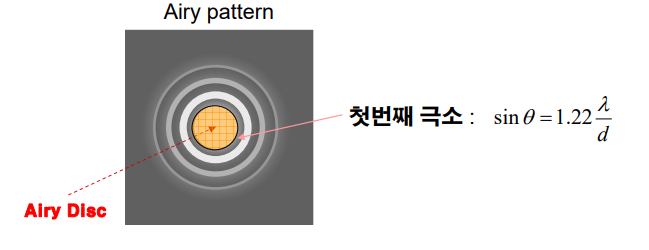
원형 구멍을 통과하는 빛은 왼쪽 그림과 같이 밝고 어두운 원형 회절 무늬를 남깁니다. 원형 구멍에 의한 중앙의 밝은 회절 무늬 크기(𝜽)는 구멍의 직경(d)에 반비례하고, 빛의 파장(λ)에 비례합니다.

 

현미경과 망원경에서의 회절, 분해능

현미경이나 망원경은 일반적으로 원형 렌즈를 사용하다 보니 가시광선의 회절 현상이 불가피합니다. 

a는 원형구멍 직경

 

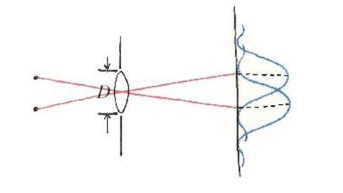
두 개의 점광원에서 나오는 빛은 렌즈를 지나 각각의 회절 무늬를 남기게 됩니다. 만약 각각의 빛에 의한 밝은 무늬 폭이 너무 넓다면 서로 겹쳐 보일 거예요. 따라서 각 빛의 밝은 무늬 폭(θ)이 좁아야 서로를 구분하기가 수월합니다. 따라서 빛의 파장이 짧을수록, 원형 구멍의 직경이 클수록, 두 상을 뚜렷하게 구분할 수 있어요. 이처럼 상을 구분하는 렌즈의 능력을 '분해능'이라 합니다. 

(좌)낮은 분해능 (우)높은 분해능

 

현미경이나 망원경의 분해능은 사용하는 파장이 짧아질수록, 렌즈의 크기가 커질수록 우수해집니다. 빨간 빛보다 파란 빛으로 보았을 때 두 상이 잘 분리되어 보여요. 이는 빨간 빛보다 파란 빛의 분해능이 우수하기 때문입니다. 이처럼 분해능은 파동의 파장이 짧을수록 우수해집니다. 

 

픽셀의 시초, 점묘법

 

쇠라는 디지털 시대를 내다본 선각자로 평가됩니다. 디지털 이미지와 동일한 방식으로 그림을 그렸기 때문이죠. 쇠라는 왜 작은 색점들을 캔버스에 일일이 손으로 찍어 촘촘히 채워가는 기계적인 방식으로 그림을 그렸던 걸까요? 쇠라의 작품 속 입자들은 작은 색점이지만 일정한 거리를 두고 그림을 바라보는 감상자의 눈에는 옆에 있는 색점들과 서로 섞여서 특정한 색으로 보입니다. 즉 그림을 보는 감상자의 눈이 색을 광학적으로 혼합합니다. 두 색이 섞여 보이지만 실제로는 색을 혼합하지 않았기 때문에 어둡거나 탁해지지 않아요. 따라서 쇠라는 점묘법만이 채도를 낮추지 않고 순수한 색을 표현할 수 있는 최상의 방법이라는 확신을 갖게 된 거죠.

 

멀리서 보면 강아지이지만, 가까이서 보면 하나하나의 점으로 보입니다. 이 경우엔 눈의 수정체가 원형 렌즈의 역할을 해요. 멀리서 볼수록 수정체와 하나하나의 점들이 이루는 각도가 줄어들다가 수정체의 분리각(𝜽=1.22λ/d)보다 작아지는 순간, 점들은 분리돼 보이지 않고 합쳐져 보입니다. 가까이서 봤을 때는 수정체와 하나하나의 점들이 이루는 각도가 수정체의 분리각(𝜽=1.22λ/d) 보다 훨씬 커지기 때문에 점들이 분리되어 보입니다.

 

2) 회절 격자(=다중 슬릿)

슬릿의 개수에 따른 회절 무늬 비교

 

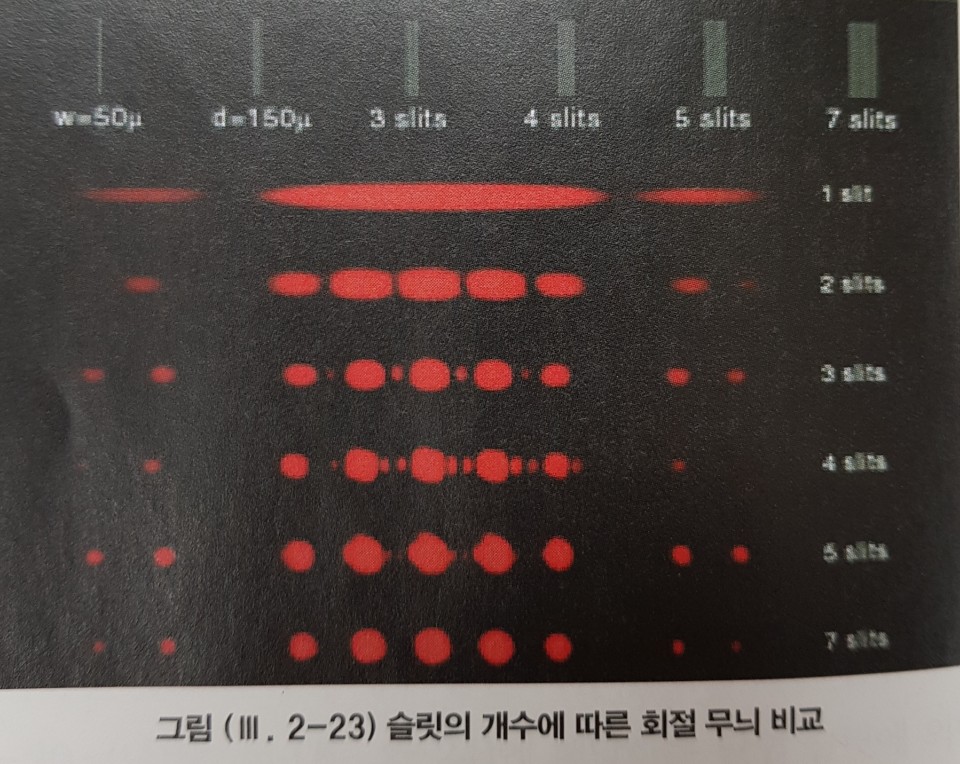
그림을 보면 슬릿의 개수가 많아질수록 밝은 무늬들의 폭이 줄어들면서 무늬 간의 분리가 선명하게 잘됨을 확인할 수 있습니다. 이처럼 슬릿의 개수가 많을수록 빛을 분해하기 쉬워요.

 

R(색분해능) = mN (m: 차수, N: 슬릿 개수)

 

위 식은 슬릿의 개수가 많을수록 빛을 분해하기 쉽다는 걸 의미합니다. 따라서 여러 파장이 혼합된 빛이 이중 슬릿에 들어갔을 때는 색분해가 되지 않지만, 회절 격자에 의해서는 그림과 같이 파장별로 분해 돼요.

 

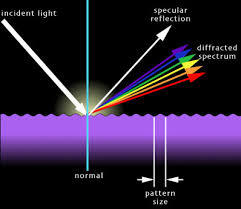
CD 표면에 나타나는 무지개 빛은 CD 표면(=회절 격자)에서 파장별로 분리된 빛들입니다.

 

① 분광기

 

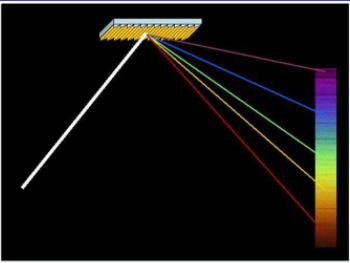
분광기는 회절 격자 구조이기 때문에 빛을 파장별로 분리할 수 있는 장치입니다.

 

② 생명에서 관찰되는 회절격자

공작의 깃털, 모르포 나비, 전복 껍데기

 

 

카멜레온은 변색을 통해 위장할 줄 아는 파충류입니다. 카멜레온의 놀라운 변색은 외피를 이루는 격자의 간격이 변함으로써 발생하는데, 그 간격은 혈압과 근육의 긴장 같은 생리적 요소를 통해서 조절돼요. 

 

황금가면 - 김동률

https://youtu.be/rS3xQQyXnUY?si=6GWrcaxyba8jyKhl 

 

희망을 안고 가다가도 좌절에 엎어지며, 닿을 듯 말 듯한 목표를 향해 우리는 수없이 흔들립니다. 때로는 '왜 하필 내게 이런 시련이 뒤따르는 걸까'란 생각에 모든 게 밉고 싫어지면서 다 포기하고 싶기도 해요. 그러나 파동을 앞으로 나아가게 했던 것은 주기적인 진동, 끊임없는 흔들림이었듯이 우리 역시 목표를 향해 앞으로 나아가는 데 있어 끊임없이 흔들릴 수밖에 없습니다. 모름지기 내 가슴을 떨리게 하는 목표야말로 삶에 굴곡을 만드는 법. 그렇기에 어떠한 역경과 냉소가 우리의 삶을 뒤흔들지라도 맘껏 흔들리되 발걸음을 멈추지 맙시다. 좌절에 엎어질지라도 '이는 성공의 반대가 아닌 성공의 일부'라 여기며 다시 일어나 가던 길을 묵묵히 걸어갑시다. 오늘도 물리를 통해 인생을 배웁니다.