[고급물리학] 관성모멘트와 돌림힘으로 설명하는 회전 운동 {돌림힘, 관성모멘트, 각운동량}

2024.03.29 - [2024 고급물리학] - [고급물리학] 입자계의 운동 {운동량 보존 법칙, 운동량과 충격량, 질량 중심}

[고급물리학] 입자계의 운동 {운동량 보존 법칙, 운동량과 충격량, 질량 중심}

 

지금까지는 직선 방향의 병진 운동만을 분석했습니다. 하지만 물체는 회전 운동도 하죠. 자동차와 자전거의 바퀴, 체조 선수가 돌리는 후프 등의 회전 운동에서 태양계 행성의 운동이나 은하의 공전처럼 아주 큰 규모의 회전 운동에 이르기까지 회전 운동은 매우 다양한 형태로 우리 생활 속에서 찾아볼 수 있습니다. 이러한 회전 운동을 설명하기 위해서는 돌림힘과 관성모멘트 등과 같은 새로운 물리량들이 필요하며 그 양들 사이의 관계로 구성된 운동 법칙을 적용해야 합니다.

 

학습 목표

• 회전 운동에서 각변위, 각속도, 각가속도 사이의 관계를 수식으로 표현할 수 있고 병진 운동과 회전 운동을 비교하여 설명할 수 있다.
• 관성모멘트, 각운동량, 돌림힘 등의 정의를 이해하고 회전 동역학에 관한 법칙들을 유도할 수 있다.

 

물리학 전개도

 

판서 조직도

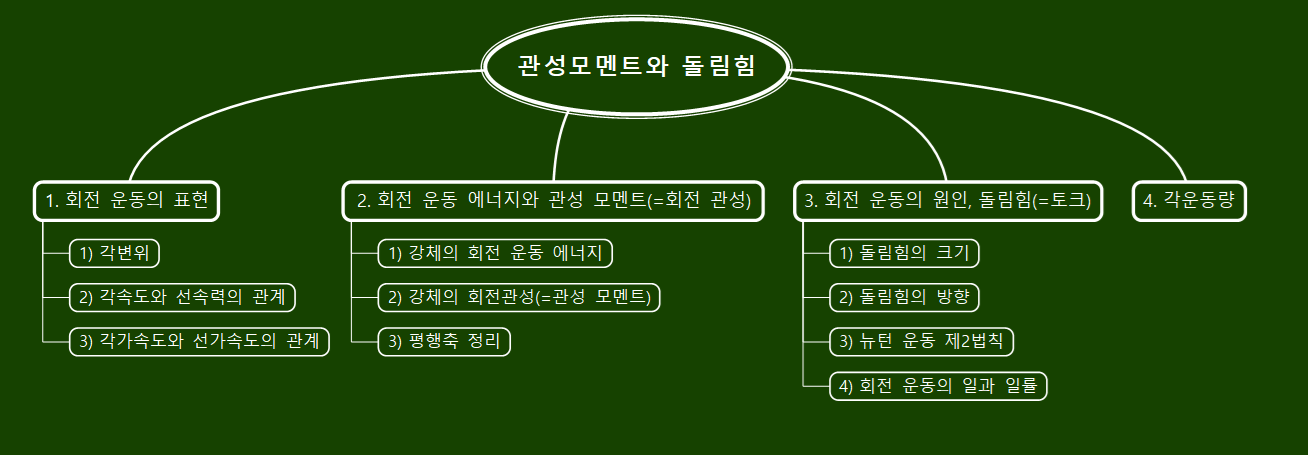
1. 회전 운동의 표현

물체가 고정된 축을 중심으로 회전하는 운동을 한다면, 그 운동 형태는 병진 운동과 다르기에 회전 운동을 설명하는 데 다른 물리량들이 필요합니다.

 

1) 각변위

 

각변위는 변위에 대응되는 물리량입니다. 각변위는 각도를 의미하는 것으로, 평면에서 각도는 각 𝜽에 의해 펼쳐지는 호의 길이 S를 원의 반지름 r로 나눈 값으로 정의합니다. (𝜽=S/r) 

 

2) 각속도와 선속력의 관계

 

각속도의 방향은 회전 방향으로 오른손 네 손가락을 감아쥘 때 엄지손가락이 가리키는 쪽입니다. 선속력과 각속도의 관계는 'v=rw' 이기 때문에 같은 각속도로 회전할 경우 회전축으로부터 거리가 멀어질수록 선속력이 커집니다.

 

3) 각가속도와 선가속도의 관계

 

회전 운동을 설명하는 물리량인 각변위, 각속도, 각가속도는 각각 병진 운동에서의 변위, 속도, 가속도에 대응됩니다. 이것을 이용하면 각가속도가 일정한 회전 운동을 등가속도 직선 운동에 대응할 수 있어요.

 

롤러코스터 증후군

롤러코스터 탑승객에게 처음부터 짜릿한 느낌을 주기 위해 평면 궤도에서 g의 가속도로 출발시킨다고 합시다. 흥분을 더욱 고조시키기 위해 궤도의 첫 부분은 원호를 그리도록 할게요. 원호를 따라 가속되는 동안 구심가속도는 급격히 증가합니다. 원호를 따라 잰 각도가 세타인 점 p에서 알짜가속도의 크기 a가 4g에 도달할 때 롤러코스터가 직선 궤도를 따라 움직이도록 설계합니다.

(1) 점 P에서 a가 4g이려면 원호가 이루는 각도 세타는 얼마이어야 하는가?

 

 

 

(2) 점 P와 그 직후의 점에서 탑승객의 알짜가속도의 크기 a는 얼마인가?

 

 

 

롤러코스터 증후군은 탑승객의 가속도가 갑자기 커지거나 작아지는 등 급격하게 변화할 때 나타날 수 있습니다. 이때 두개골에 대해 상대적으로 뇌가 움직여서 두개골과 뇌를 연결하는 정맥이 끊어질 수 있어요.

 

2. 회전 운동 에너지와 관성 모멘트(=회전 관성) 

운동 에너지, 질량, 힘과 같은 물리량들 역시 회전 운동에서는 새롭게 정의된 물리량들로 치환하는 게 낫습니다. 먼저 고정된 축 주위를 도는 강체의 회전 운동 에너지를 정의해보죠. '강체'란 회전 운동하는 동안 물체를 구성하는 입자들 사이의 거리가 변하지 않는 물체를 말합니다. 통상 회전 운동을 설명할 때 물체를 강체로 간주해요. 강체가 N개의 입자들로 구성되어 있고, 입자들 모두 각속도 w로 움직이고 있는 상황이라 가정합시다.

1) 강체의 회전 운동 에너지

 

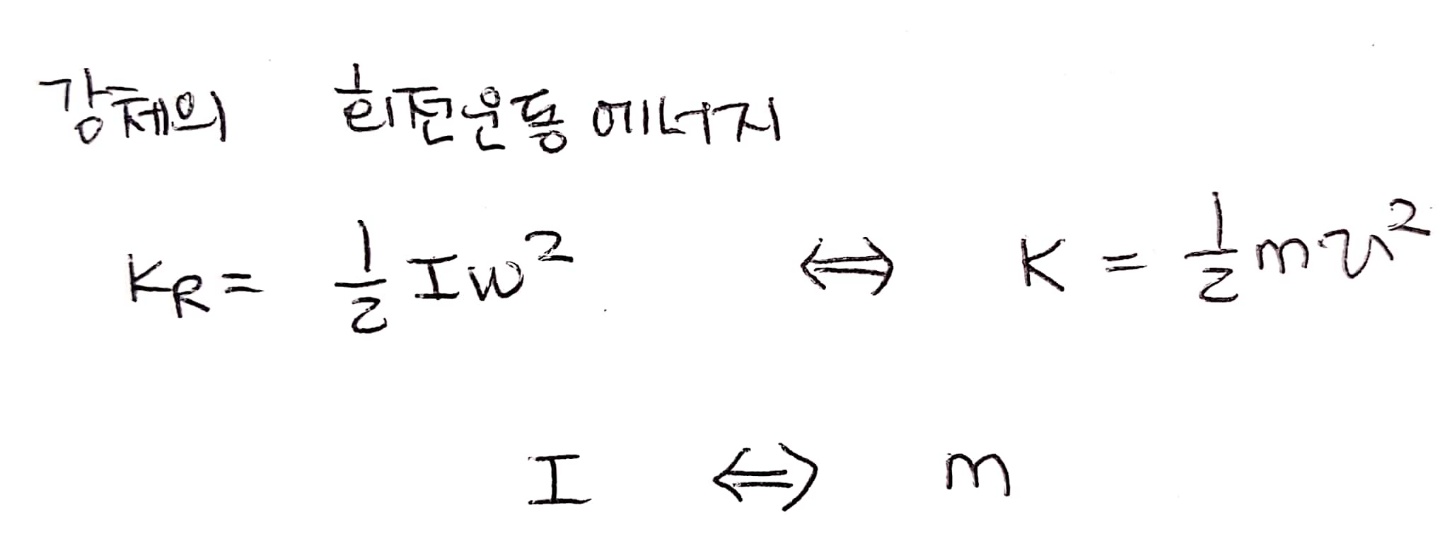
2) 강체의 회전관성(=관성 모멘트)

(가) 고리 또는 얇은 원통 껍질 (나) 두께가 있는 원통 (다) 속이 찬 원통 또는 원판 (라) 중심을 지나고 길이에 수직한 축에 대해 회전하는 속이 찬 원통 (마) 중심을 지나고 길이에 수직한 축에 대해 회전하는 가느다란 막대 (바) 속이 찬 공 (사) 공 껍질 (아) 지름을 축으로 하여 회전하는 고리 (자) 중심을 지나고 면에 수직한 축에 대해 회전하는 얇은 판

 

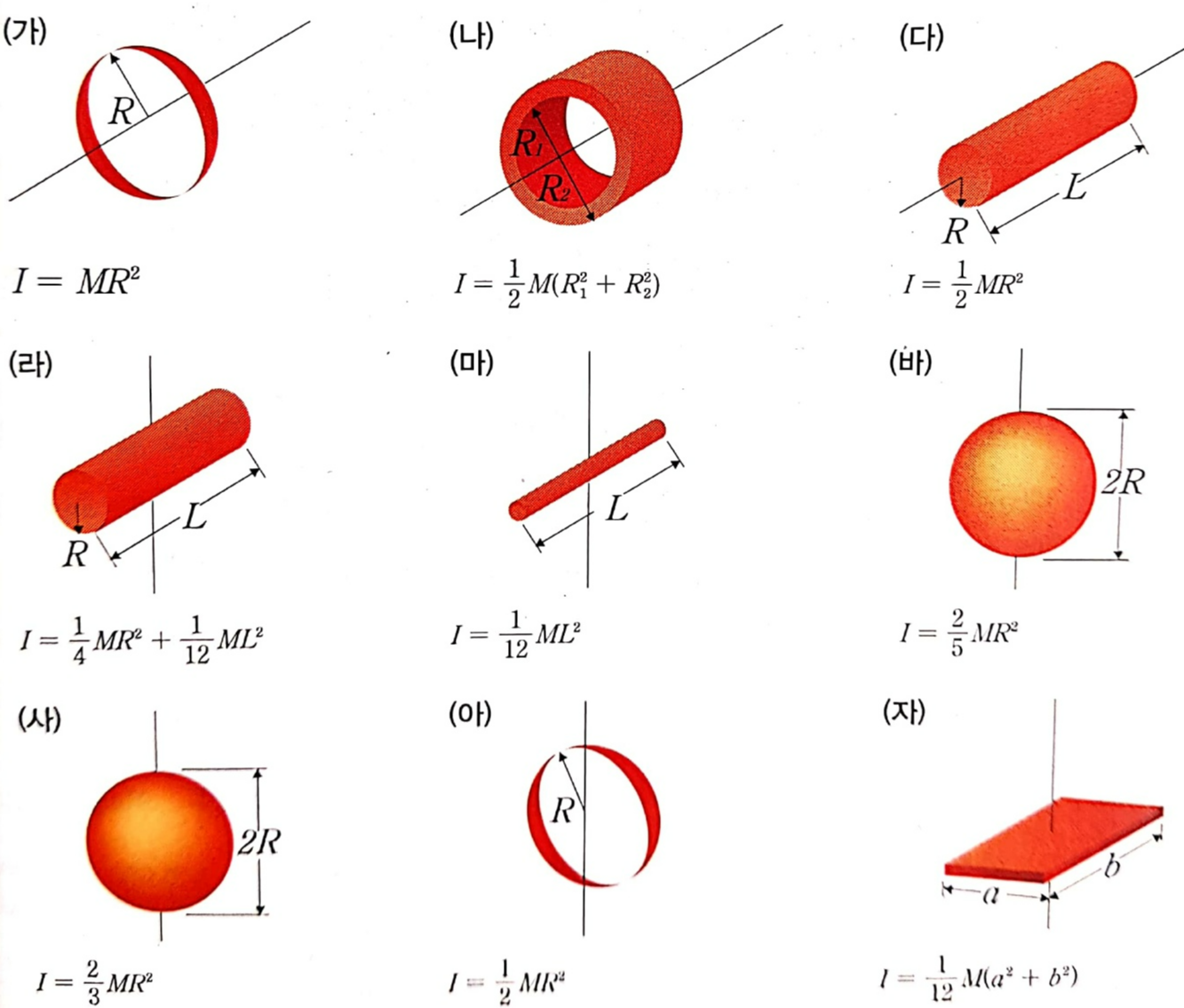
'(다), (라)', '(가), (아)'와 같이 동일한 강체일지라도 회전축의 방향에 따라 회전 관성의 크기가 달라짐을 확인하세요.

 

3) 평행축 정리

강체의 질량중심을 지나는 회전축에 대한 회전관성을 아는 경우, 평행한 다른 축에 대한 회전관성을 쉽게 구할 수 있습니다. 질량중심을 지나는 회전축에 대한 회전 관성이 Icm일 때 그 축으로부터 h만큼 떨어진 평행한 다른 축에 대한 회전 관성은 다음과 같습니다.

 

 

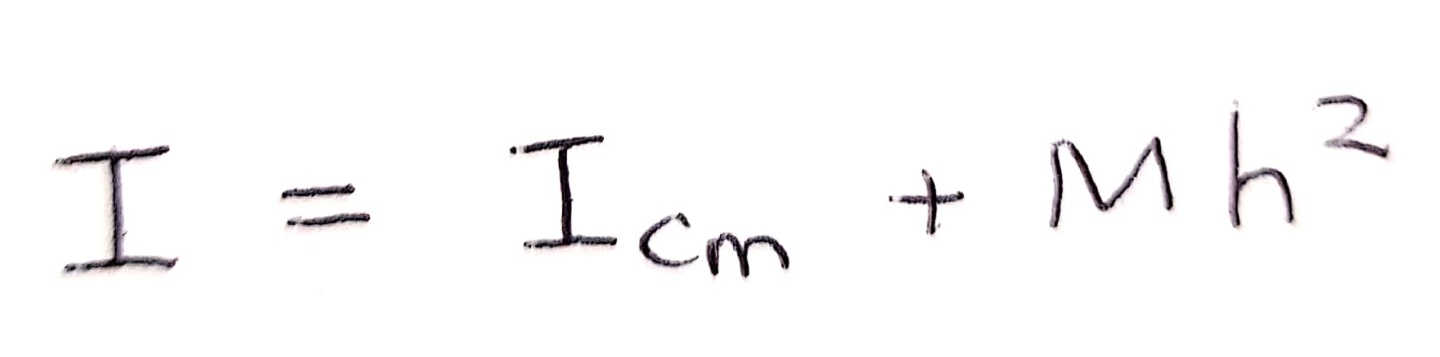
다음 막대의 회전관성을 두 가지 방법으로 구하겠습니다.

 

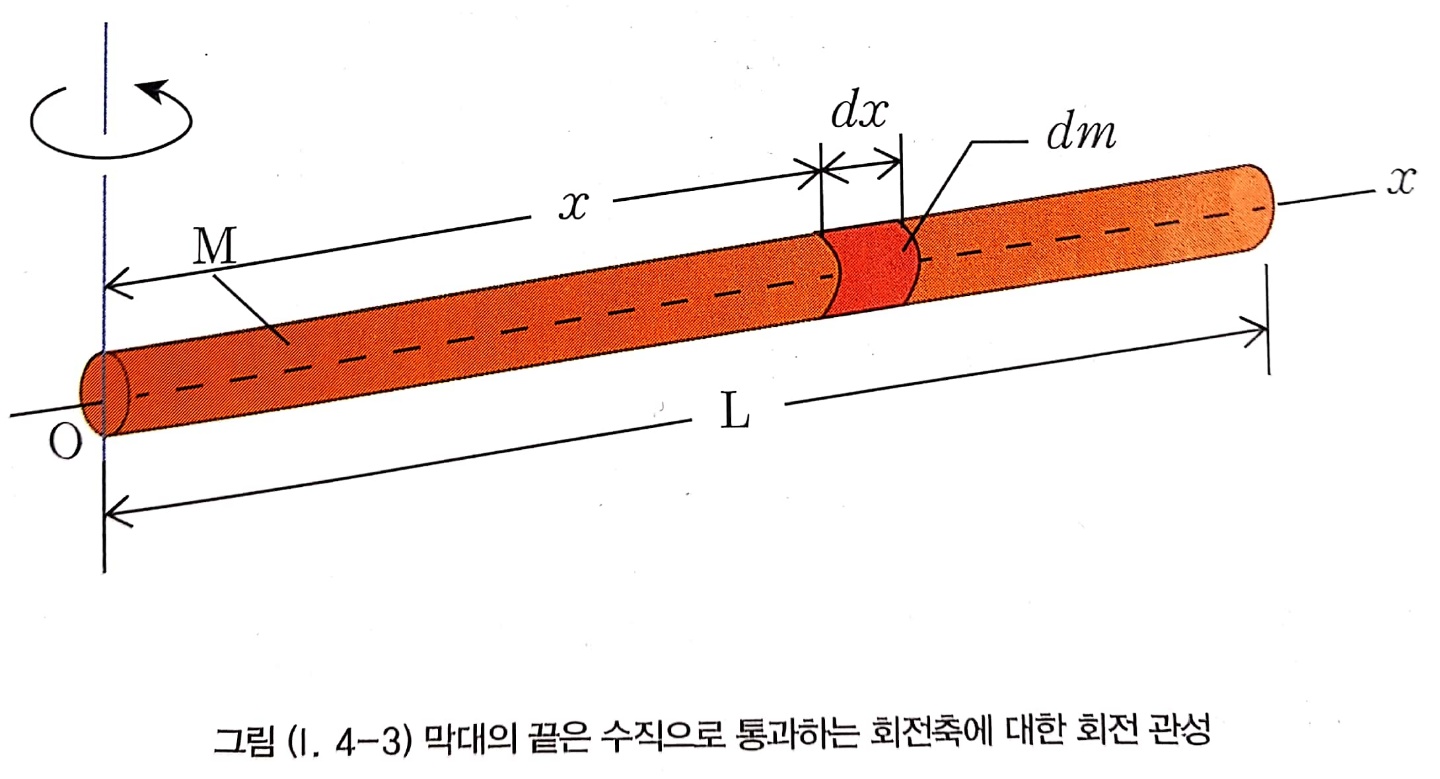
① 회전관성의 정의를 이용해서 구하기

 

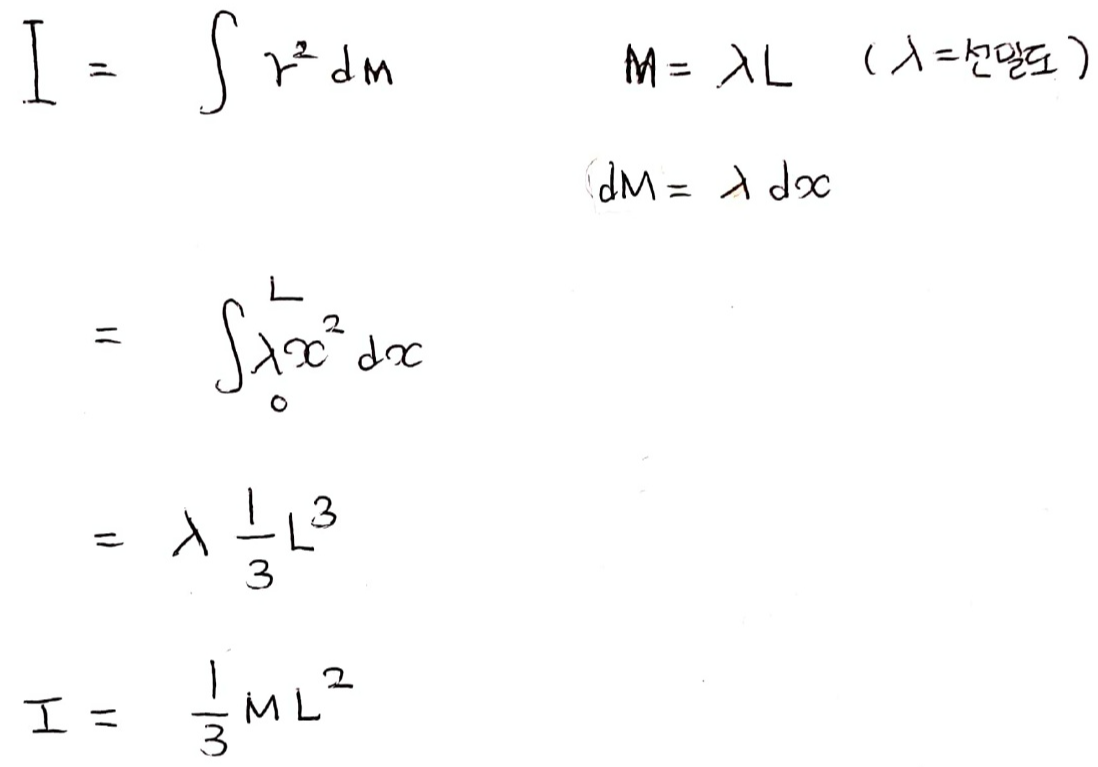
② 평행축 정리를 이용해서 구하기

 

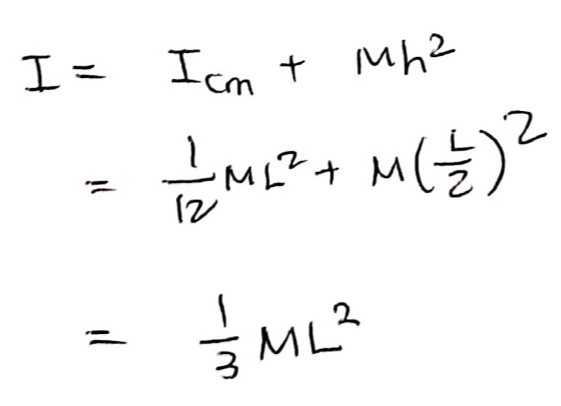
3. 회전 운동의 원인, 돌림힘(=토크)

 

병진 운동의 원인, 힘에 대응되는 회전 운동의 원인을 '돌림힘'이라 합니다. 

 

1) 돌림힘의 크기

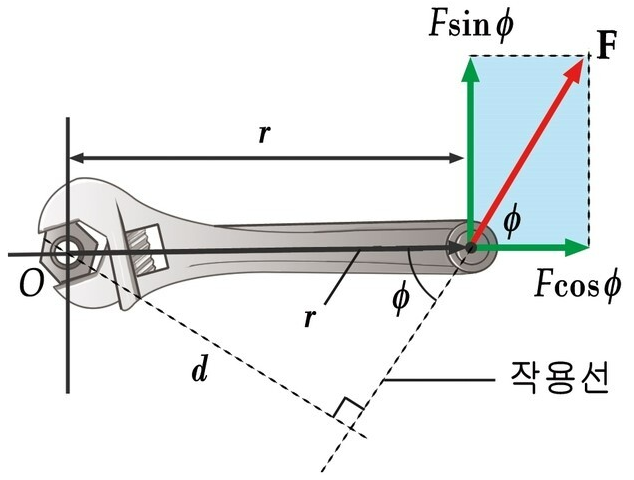
그림과 같이 볼트에 스패너를 장착하여 힘 F로 조이거나 풀면 볼트에는 돌림힘이 작용하여 볼트 중심을 지나는 축(=회전축 O)을 중심으로 회전합니다. 스패너에 가해진 힘 F는 두 성분(Fcosϕ, Fsinϕ)으로 분해할 수 있어요. 그러나 Fcosϕ는 오른쪽으로 당기기만 할 뿐, 스패너를 회전시키는 힘의 성분이 아닙니다. 따라서 돌림힘은 변위 r에 수직한 힘(Fsinϕ)만 고려합니다.

 

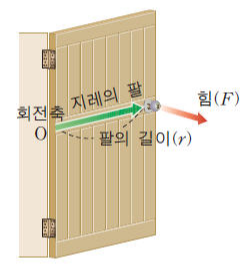
문고리가 회전축으로부터 멀리 있는 문, 가까이 있는 문이 있다고 합시다. 어느 문이 열기 쉬운가요? 같은 힘으로 당겼을 때 문고리가 회전축에 멀리 있는 문이 열기가 더 쉽습니다. 그 이유는 회전축으로부터 멀리 떨어진 지점에 힘을 가했을 때 돌림힘이 더 크기 때문이죠. 이처럼 돌림힘의 크기는 회전축과의 거리에 비례합니다.

 

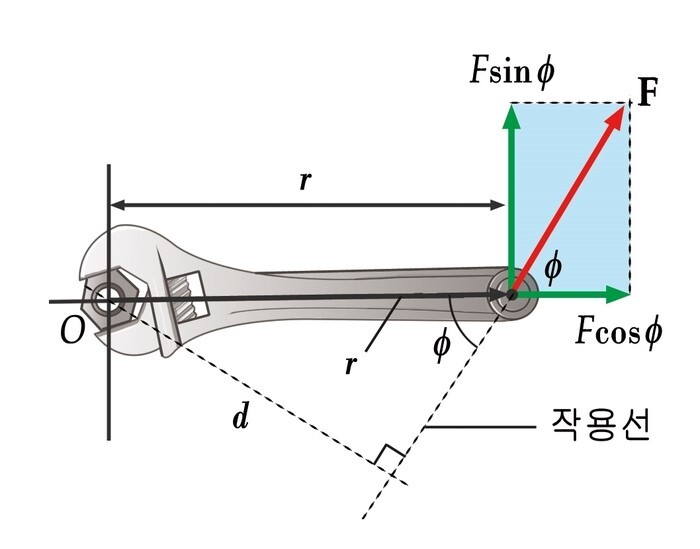
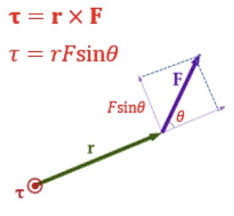
정리하면 돌림힘의 크기는 회전축 O로부터 힘이 작용하는 점까지 거리 r과 힘 F, 그리고 r과 F가 이루는 각 ϕ에 따라 결정됩니다. 즉, 돌림힘을 τ라 하면 τ=rFsinϕ 와 같아요. 돌림힘은 힘과 거리를 곱한 물리량으로 단위는 N·m인데, 차원만 놓고 보면 힘이 한 일과 똑같습니다만 명백히 다른 개념입니다.

 

2) 돌림힘의 방향

 

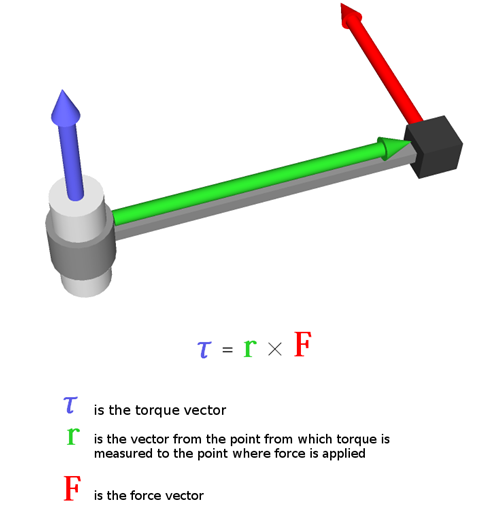
돌림힘의 방향은 오른손 법칙으로 정해요. 회전하는 방향으로 오른손을 감쌌을 때 엄지손가락이 가리키는 방향이 돌림힘의 방향입니다. 윗 그림의 경우 힘 F 방향으로 돌리면(=반시계 방향) 돌림힘의 방향은 지면에서 나오는 윗방향이 됩니다.

 

3) 뉴턴 운동 제2법칙

 

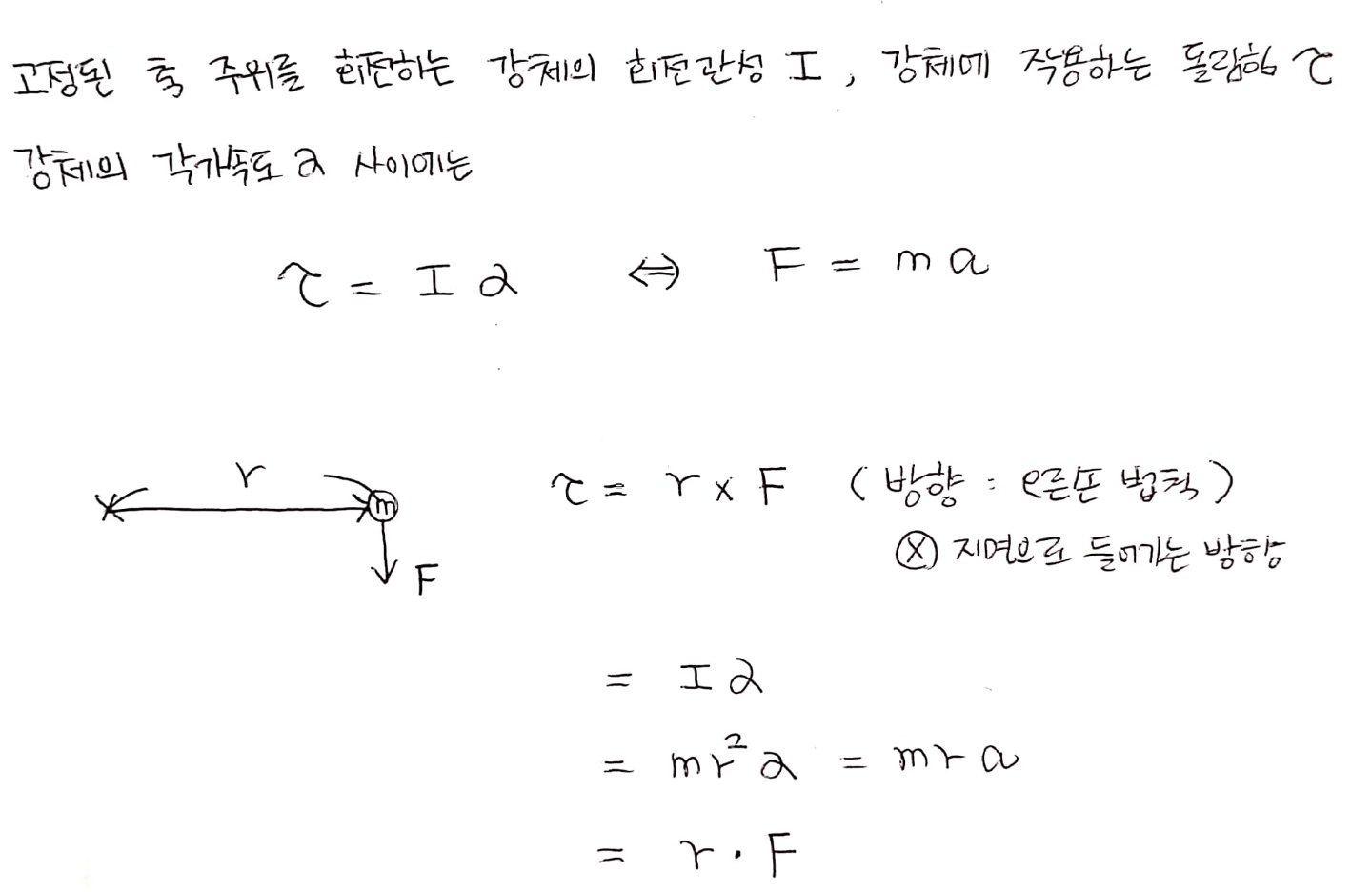
4) 회전 운동의 일과 일률

일과 에너지 관점에서 강체의 회전 운동을 다뤄봅시다.

4. 각운동량

회전 운동에서 회전 운동 상태를 나타내는 물리량인 각운동량 L에 대해 알아봅시다.

 

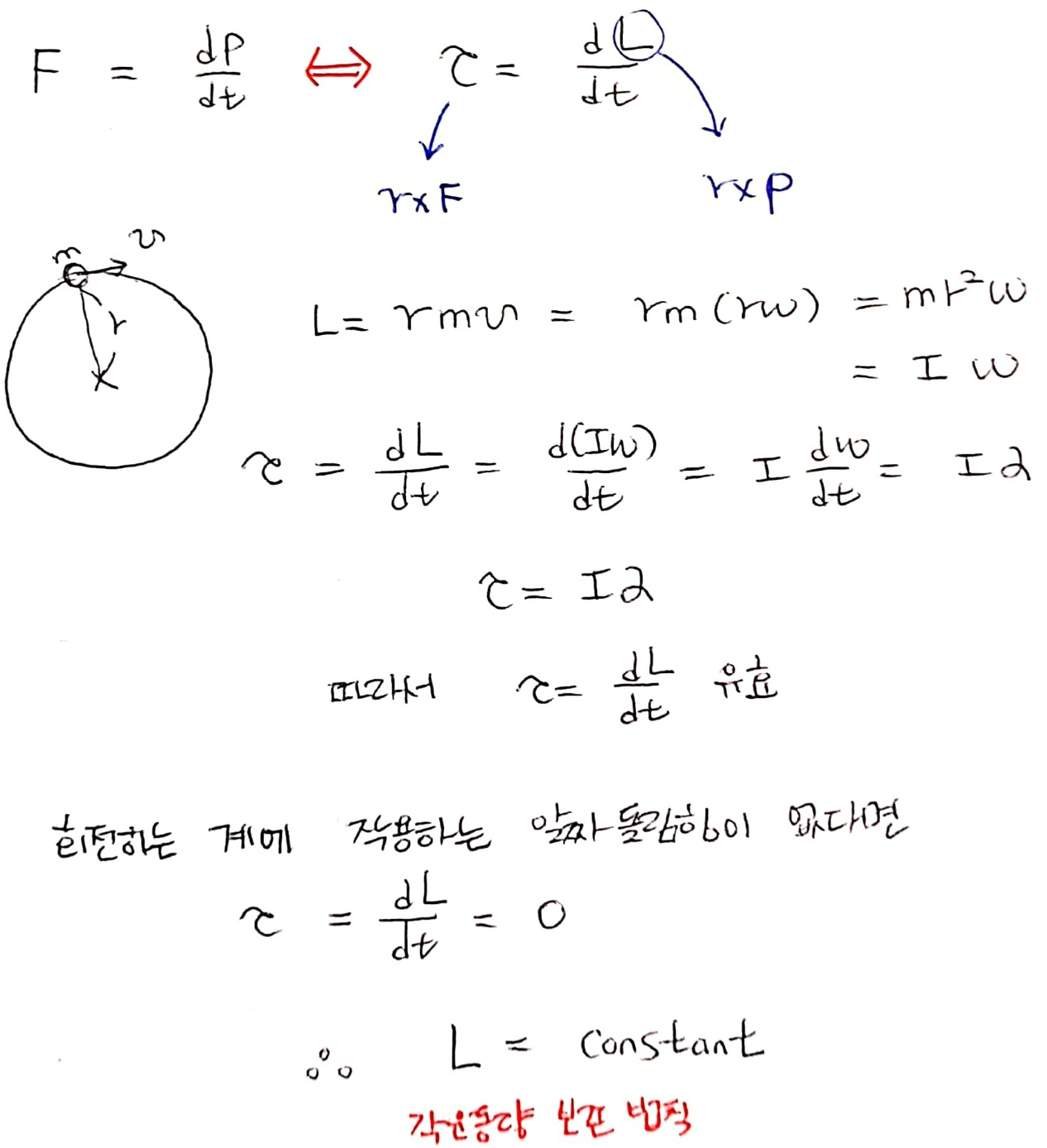
각운동량 보존 법칙은 태양을 중심으로 하는 타원 궤도를 도는 행성들의 운동을 설명합니다. 스포츠에서도 각운동량 보존의 예를 찾을 수 있어요.

 

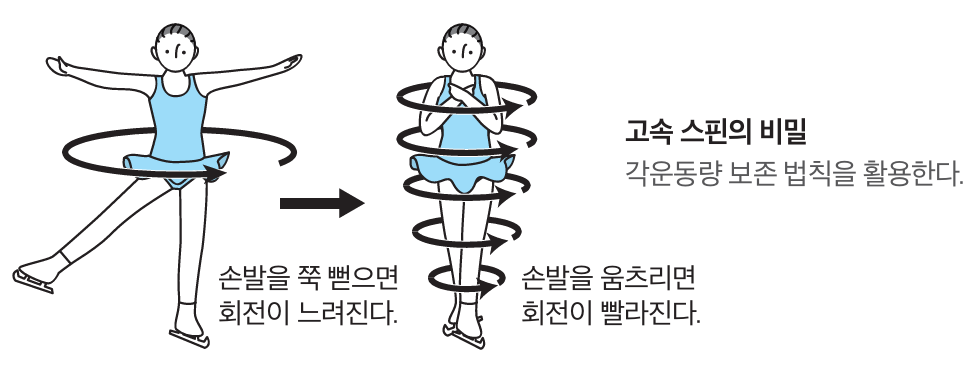
각운동량 보존 법칙은 에너지 보존 법칙처럼 거시적인 역학계뿐만 아니라 미시적인 양자계에서도 성립하는 물리학의 기본적인 법칙입니다. 특히 미시계에서 각운동량 보존 법칙의 중요성은 이루 말할 수 없어요.

 

괜찮아요 - 비투비

 

https://www.youtube.com/watch?v=vgEKwPiapwU

 

나이 들어가며 철든다고 하잖아요. 그래서 어른이 되어가는 삶은 철(鐵)을 든 만큼 무거워지는 거 같아요. 쌓여가는 시간 따라 잃을 것과 지켜야 할 것들이 하나 둘 생겨나며 묵직해져 가는 삶의 무게감. 그러한 삶의 무게감을 덜어내고 싶다가도 막상 내려놓자면 머뭇거리게 됩니다. 그렇기에 아무것도 몰라서 재고 따지지 않았던 철없는 시절이 그리울 때가 있습니다. 

 

무게중심과 구조의 안정성

 

그러나 그러한 삶의 무게감이야말로 내 삶의 중심을 잡아주는 묵직함이었습니다. 숱하게 스쳐 지났던 지난한 일에 오뚝이처럼 다시 일어설 수 있게 균형감을 잡아주었던 건 내 자아 깊은 곳을 차곡차곡 채워갔던 삶의 묵직함이었습니다.

내용 체크 문제

1. 질량 M, 반지름 R인 균일한 원판이 고정된 축에 끼워져 회전한다. 질량 m인 토막이 원판 테두리에 감긴 줄에 연결되어 있다.

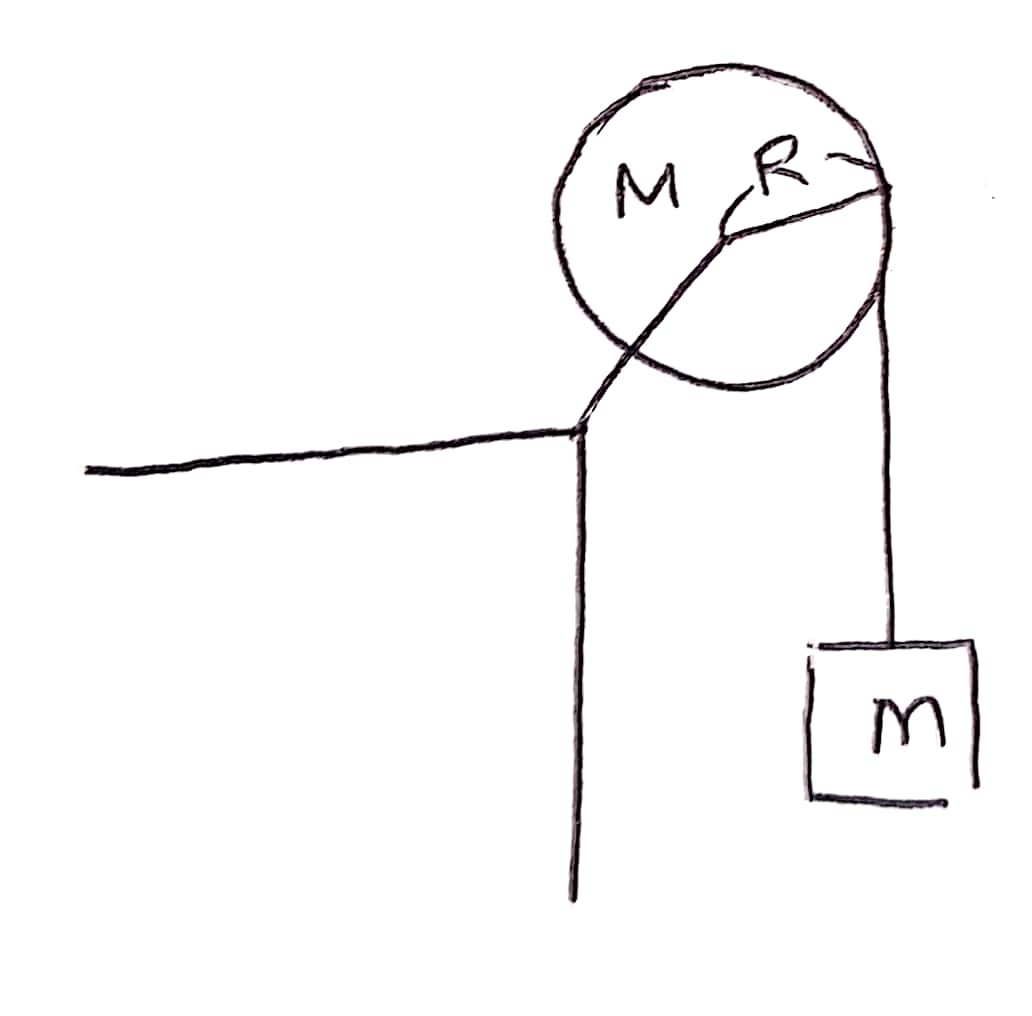
낙하하는 토막의 가속도, 원판의 각가속도 그리고 줄의 장력을 구하여라. (단, 줄은 질량이 없고 미끄러지지 않으며 축과 원판 사이의 마찰도 없다.)

 

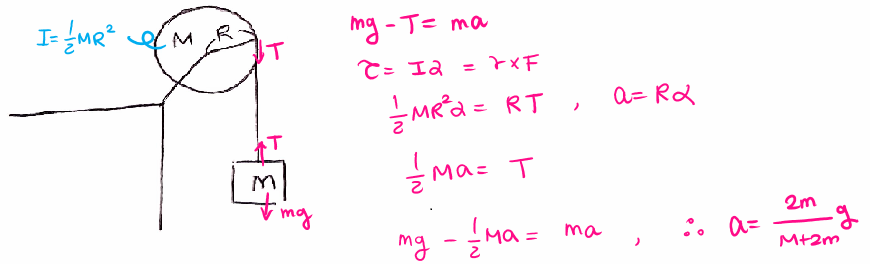
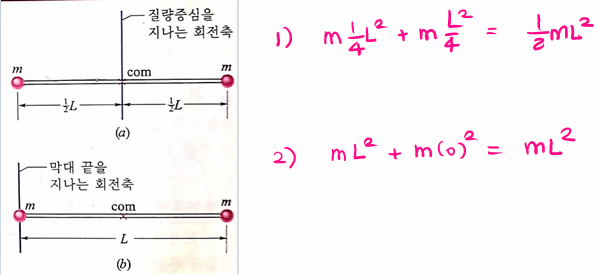
2. 그림처럼 질량이 m인 두 입자가 길이가 L이고 질량이 거의 없는 막대로 연결되어 강체를 구성하고 있다.

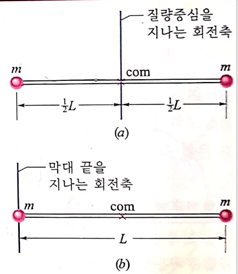
(1) 막대의 질량중심을 지나는 축에 대한 회전관성을 구하여라

 

(2) 막대 끝을 지나는 축에 대한 회전관성을 구하여라.

 

 

3. 그림과 같이 질량 M, 반지름 R인 원판에 질량 m인 총알이 속력 v로 원판의 지름 방향과 𝜽의 각도를 이루며 날아와 원판 테두리에 박혔다.

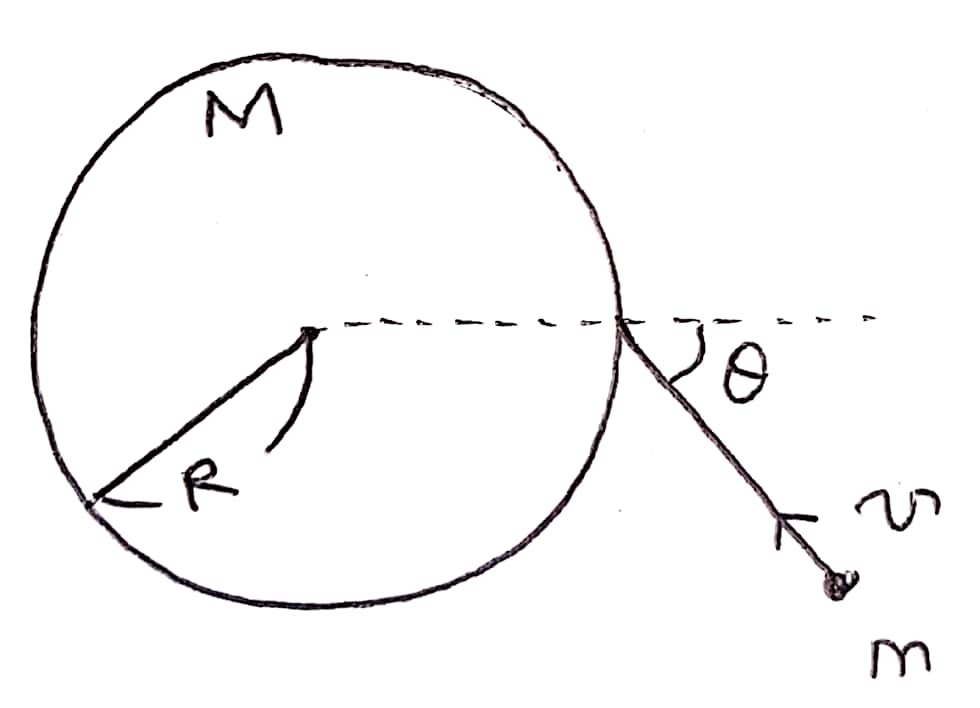
원판이 지면에 수직으로 중심 O를 지나는 회전축 주위로 마찰 없이 회전할 수 있을 때, 총알이 박힌 후 원판의 각속도 크기를 구하시오.