[고급물리학] 입자계의 운동 {운동량 보존 법칙, 운동량과 충격량, 질량 중심}

2024.03.28 - [2024 고급물리학] - [고급물리학] 일과 에너지의 관계 {보존력과 비보존력}

[고급물리학] 일과 에너지의 관계 {보존력과 비보존력}

 

학습 목표

• 운동량 보존 법칙을 이용하여 충돌 현상을 설명할 수 있다.
• 질량 중심의 정의를 이해할 수 있다.
• 질량 중심을 이용하여 물체의 운동을 설명할 수 있다.
• 질량이 변하는 물체의 운동을 이해하여 로켓의 운동을 설명할 수 있다.

 

물리학 전개도

 

판서 조직도

 

1. 운동량 보존 법칙

1) 운동량의 정의

 

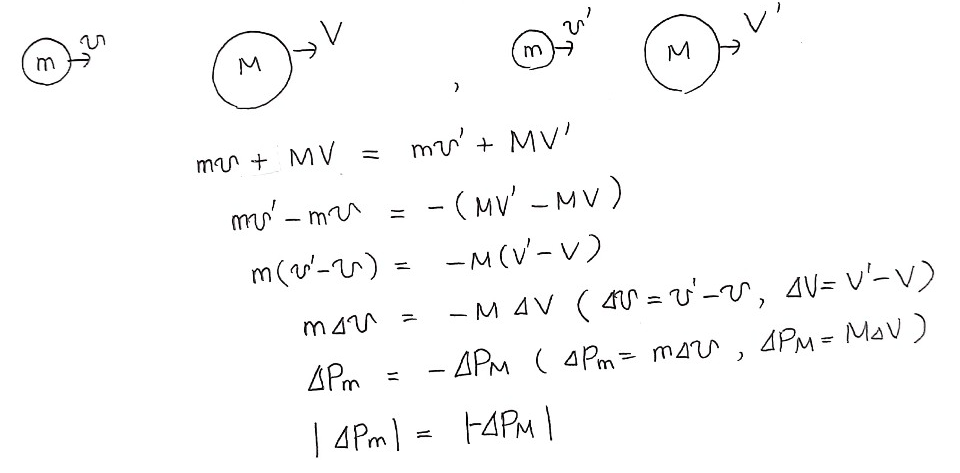
운동량은 질량이 m인 물체가 속도 v로 운동할 때 가지는 물리량으로써 크기와 방향을 모두 갖습니다. 기호는 P(pimentum), 단위는 kg·m/s

 

2) 운동량 보존 법칙, 사실은 뉴턴 운동 제3법칙

 

 

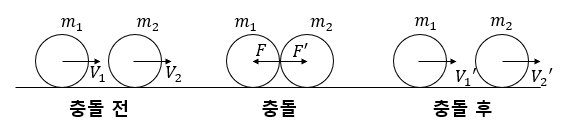
두 물체가 충돌하는 시간(△t) 동안 서로에게 작용하는 힘들은 '작용 반작용 관계'에 있기 때문에 크기가 같고, 방향은 서로 반대입니다.

 

 

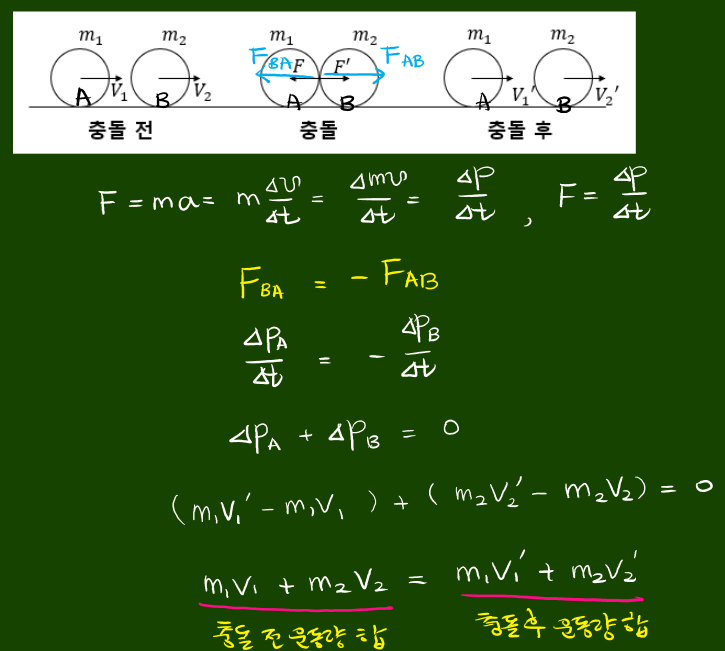
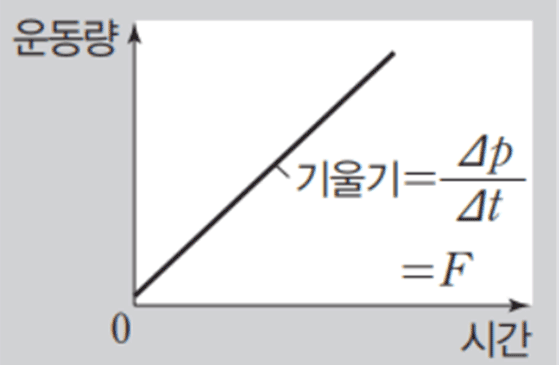
운동량-시간 그래프와 힘

 

2. 운동량과 충격량의 관계

1) 충격량의 정의

 

충격량은 △t동안 F가 물체에 작용할 때 물체가 받는 물리량으로써 크기와 방향을 모두 갖습니다.

기호는 I(Impulse), 단위는 N·s

 

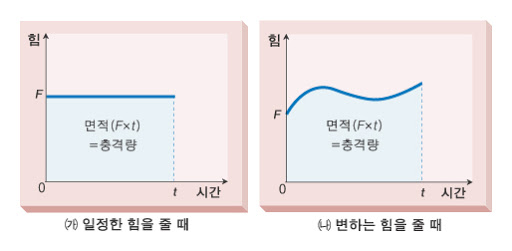
2) 운동량과 충격량의 관계, 힘에 대한 시간적 접근

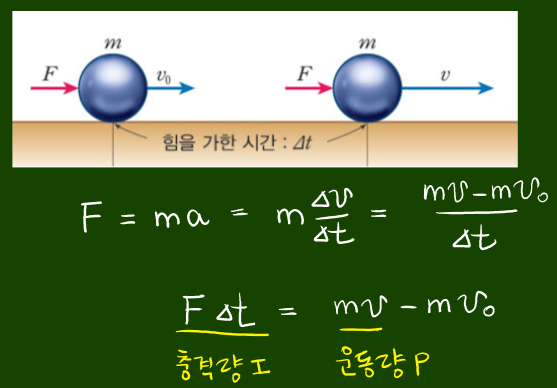
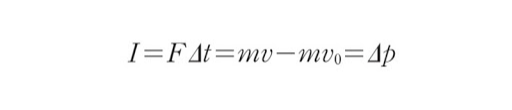
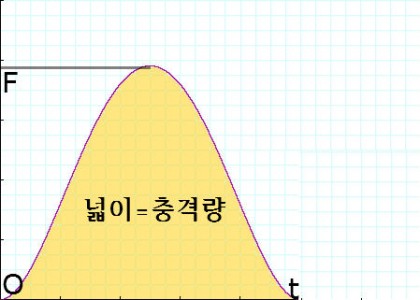
힘-시간 그래프와 충격량

 

3. 입자계의 운동

문제를 풀다 보면 이런 전제 조건을 많이 봤을 겁니다. '물체의 크기는 무시한다.' 이는 물체를 '질점'(=크기를 무시할 수 있는 점으로 여기에 물체의 모든 질량이 모여있음)으로 간주한 것이에요. 따라서 크기가 있는 실제 물체의 운동을 이해하기 위해서는 질점들로 이루어진 입자계의 운동을 이해할 필요가 있습니다.

 

1) 질량중심

질점으로 다룰 수 없는 역학계의 운동을 다룰 때는 계의 '질량중심'이라는 특별한 점을 이용해야 합니다.

 

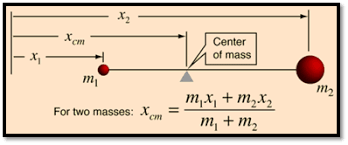
① 1차원 상 두 입자의 질량중심

 

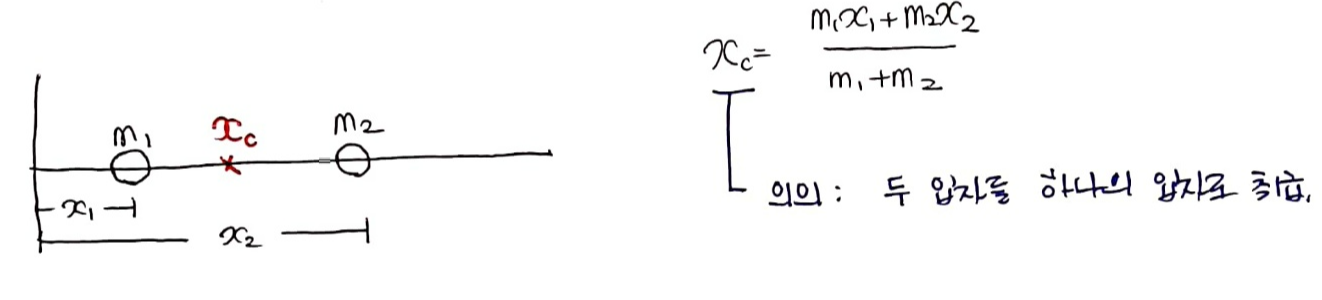
② 3차원 상 n개 입자들의 질량중심

 

2) 질량중심의 운동

 

질량중심의 운동은 입자계에 작용하는 외부 알짜힘의 영향만 받게 됩니다. 그 이유는 입자계 내부의 힘들은 '작용 반작용 법칙'에 의하여 상쇄되기 때문에 결과적으로 내부 힘에 대한 효과는 무시됩니다. 따라서 입자계의 총 질량과 질량중심의 가속도를 곱한 값은 입자계가 받는 외부 알짜힘의 크기와 같습니다. 

 

 

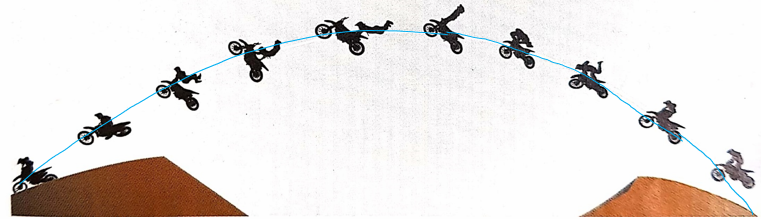
그림은 '오토바이와 선수의 질량중심'이 이동하는 경로입니다. 질량중심은 오토바이와 선수 어딘가에 있으며 선수의 움직임에 관계없이 질량중심의 이동 경로는 중력장에서 단일 물체의 포물선 운동 궤적과 동일해요. 이처럼 질량중심의 운동은 중력을 비롯한 외부 알짜힘에 의해서만 결정돼요.

 

즉, 질량중심은 입자계의 복잡한 질량 분포와 여러 힘들을 하나의 점에 작용하는 하나의 외부 알짜힘만으로 단순화하는 데 의의가 있습니다.

 

4. 입자계에서의 운동량 보존 법칙

 

 

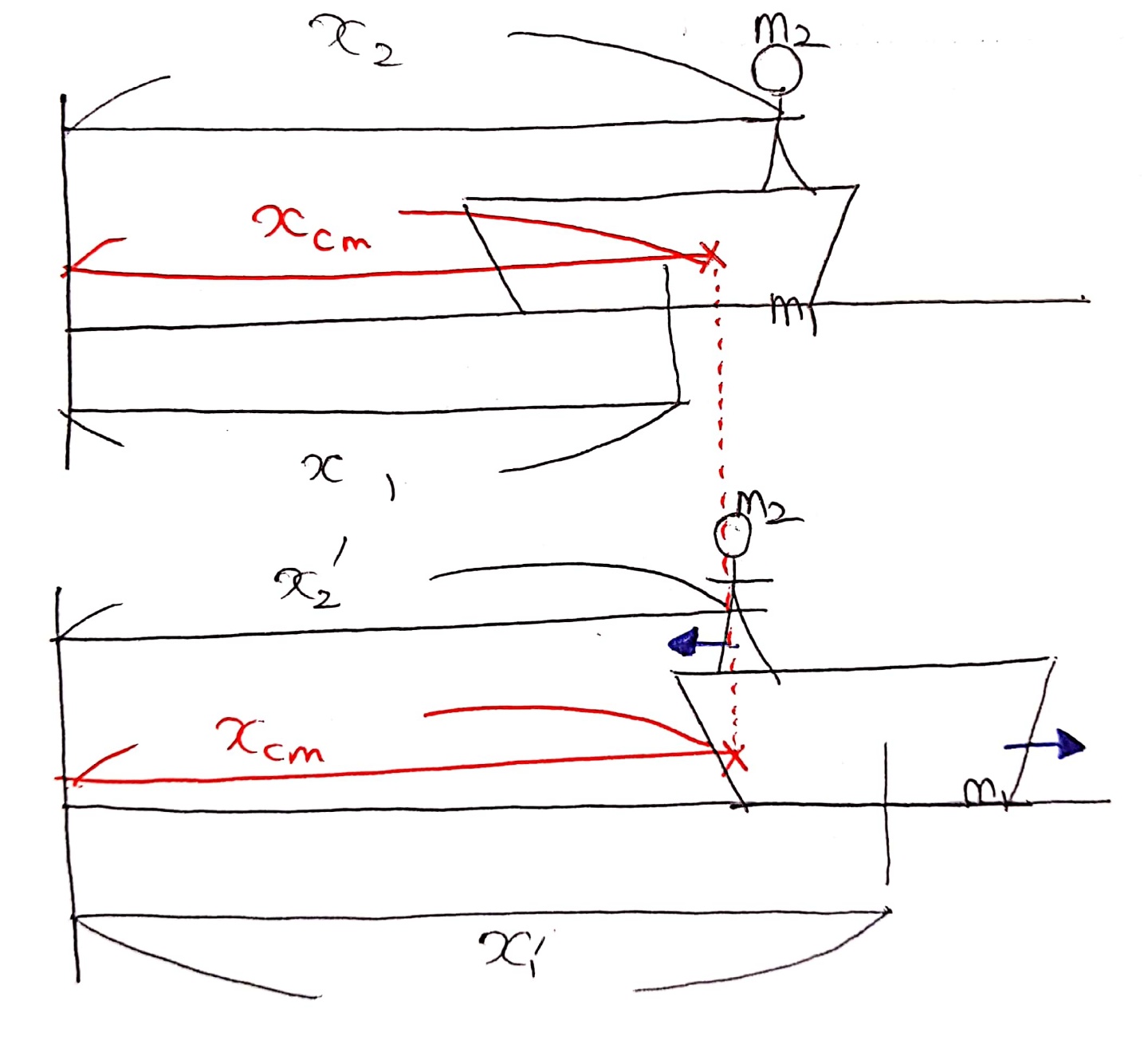
뉴턴 운동 제1법칙에 의하면 외부 알짜힘이 0이라면 정지해있는 입자계의 질량중심은 계속 정지해 있습니다. 그러나 이것이 계를 구성하는 입자들이 모두 정지해야 함을 의미하지는 않아요. 사람이 왼쪽으로 움직였을 때 질량중심의 위치가 변화되지 않으려면 배가 오른쪽으로 움직여야겠죠? 이를 운동량 보존 법칙으로 설명할게요.

 

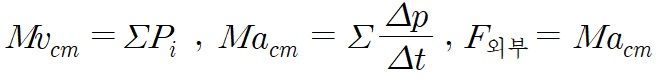
외부 알짜힘이 0인 경우 입자계의 총운동량은 일정하게 유지됩니다. 예를 들어 배와 사람으로 이루어진 입자계에 어떠한 수평 방향의 힘도 작용하지 않는다면 입자계의 수평 방향 총운동량은 0으로 보존되어야 합니다. 사람이 왼쪽으로 이동하며 생긴 운동량은 배가 오른쪽으로 이동하여 생긴 운동량으로 상쇄해야 배와 사람으로 이루어진 입자계의 총운동량이 0이 되겠죠? 이러한 입자계의 운동량 보존 법칙을 토대로 2차원 충돌 현상과 로켓 추진의 원리를 설명합니다.

 

1) 2차원 충돌

충돌은 두 물체 이상으로 이루어진 계의 내부 작용에 의해서 일어나는 현상이므로 계에 작용하는 외부 알짜힘이 0이라면 충돌하기 전과 후 총운동량이 보존됩니다. 

 

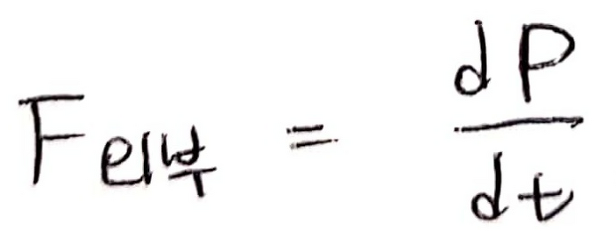
콤프턴 산란에서 활용될 2차원 충돌

충돌 전, 충돌 후 두 물체는 등속도 운동을 한다.

 

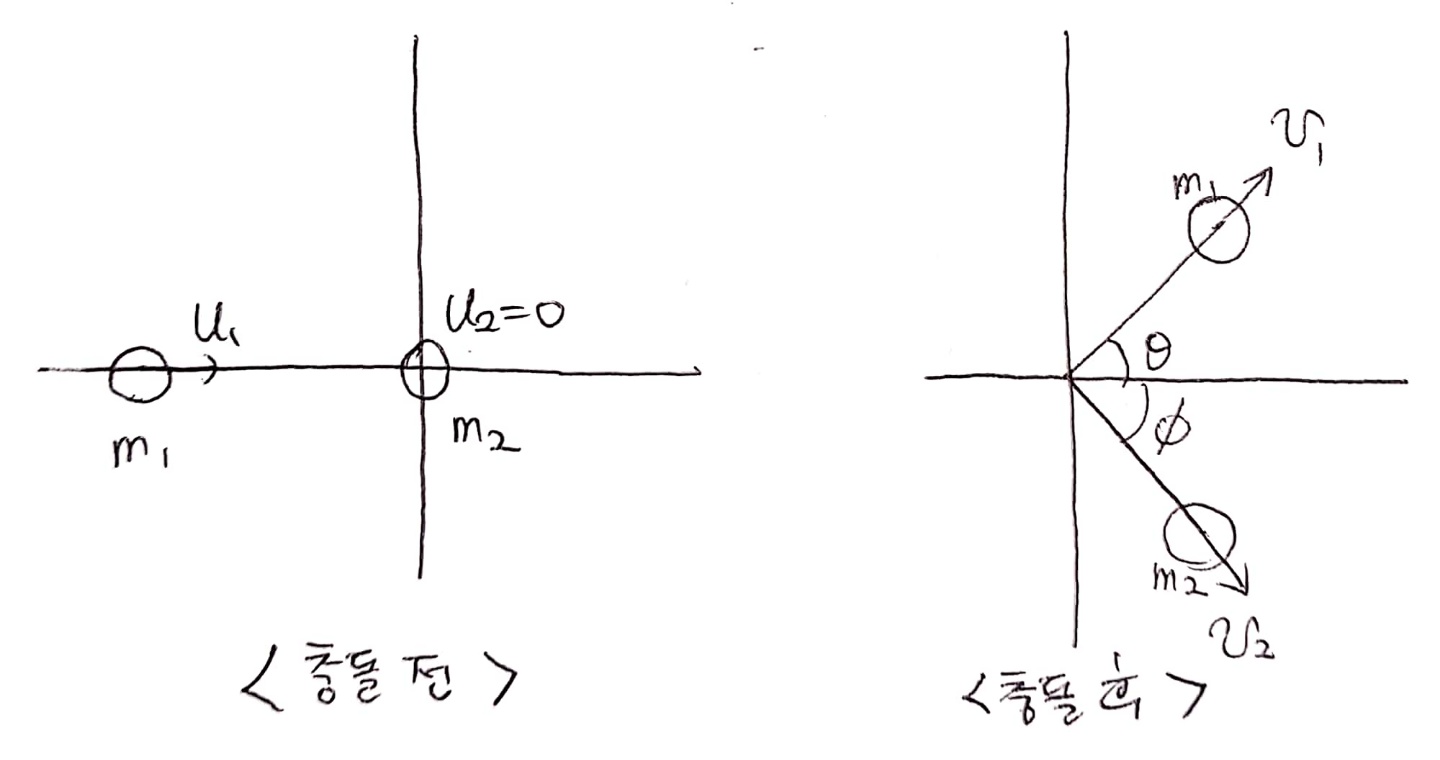
입자계에 작용하는 외부 알짜힘이 0이면 충돌 전후의 총 운동량은 보존됩니다. 

 

'탄성 충돌'하는 경우 충돌 후 두 입자 사이의 각도에 대한 일반적인 관계를 알아봅시다.

 

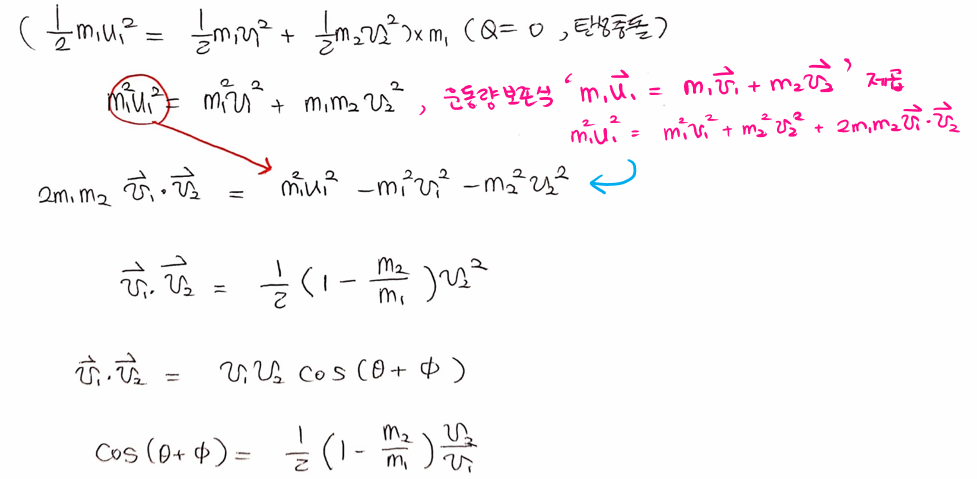
두 입자의 질량이 서로 같다면 각도가 90˚가 됨을 확인하세요.

 

2) 로켓의 운동

 

즉 로켓은 연료를 소진함으로써(=질량이 감소) 추진력을 얻게 됩니다.

 

롤린 - 브레이브 걸스

https://www.youtube.com/watch?v=cfHWIqJkEf4

 

눈빛만 봐도 설레고 좋은 사람이 있다면, 그 사람 곁에 계속 있고 싶기 마련입니다. 태양의 중력에 이끌려 그 주위를 맴도는 지구처럼, 좋아하는 사람의 눈빛에 이끌려 그의 주위를 맴도는 나 자신을 발견할 수 있죠. 그 사람의 눈빛과 마음을 훔칠 수만 있다면 좋겠다는 발칙한 생각도 갖게 됩니다. 

 

스윙 바이, 중력을 훔치다.

 

우주 멀리 무언가를 보낼 때 무엇이 필요할까요? 로켓이죠. 그러나 현재 로켓기술로는 화성까지 가기도 어려운 수준입니다. 그럼에도 불구하고 인류는 화성 너머로 수많은 로켓들을 보냈고 심지어 태양계 밖으로 나간 인공위성들도 있습니다. 이 인공위성들은 어떻게 저 멀리까지 간 걸까요? 그 비결은 바로 '스윙 바이'에 있습니다. '스윙 바이'는 말 그대로 로켓이 행성에 잠깐 다가갔다가 다시 멀어지는 건데, 이때 행성의 중력을 훔쳐서 로켓을 가속시키는 거예요. 행성의 중력을 이용해 로켓을 추진하기 때문에 로켓의 연료 사용량을 대폭 절감할 수 있습니다. 그렇다면 로켓이 행성을 스치는 것만으로 속도가 빨라지는 건 무엇 때문일까요? 답은 바로 '운동량 보존 법칙'에 있습니다.

 

스윙 바이와 운동량 보존 법칙

'스윙 바이'의 원리는 운동량 보존 법칙입니다. 행성은 정지한 채로 있지 않고, 태양 주위를 공전합니다. 행성과 로켓의 운동을 간단하게 1차원으로 근사할게요.

m = 로켓의 질량, M = 행성의 질량, v = 로켓 속도, V = 행성 공전 속도 / 거칠게 일반화한 상황

 

운동량 보존 법칙에 따라 로켓과 행성의 운동량 변화량(△P)은 같습니다. 서로의 운동량 변화량은 각자의 질량과 속도 변화량을 곱한 것이므로 행성에 비해 질량이 작은 탐사선은 속도가 크게 변화하지만, 질량이 매우 큰 행성은 속도가 거의 변화하지 않아요. 편의상 로켓의 질량을 1 행성의 질량을 1000 서로의 운동량 변화량을 1000이라 가정한다면, 행성의 속도가 1만큼 변하는 동안 로켓의 속도는 1000만큼 바뀝니다. 물론 로켓의 속도는 로켓과 행성의 상대적인 운동 방향에 따라 느려질 수도 빨라질 수도 있어요.

 

행성과 로켓의 상대적인 운동 경우의 수

 

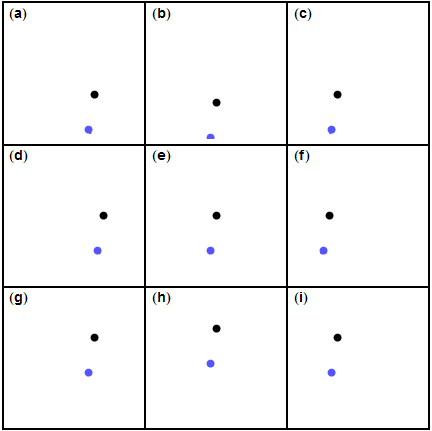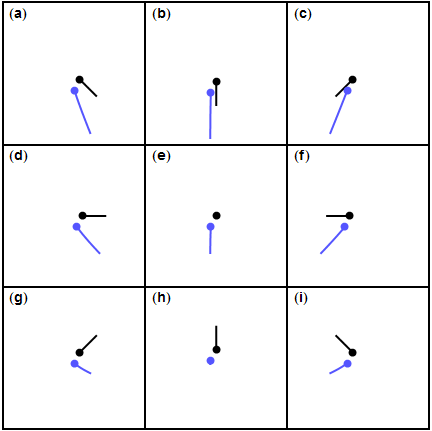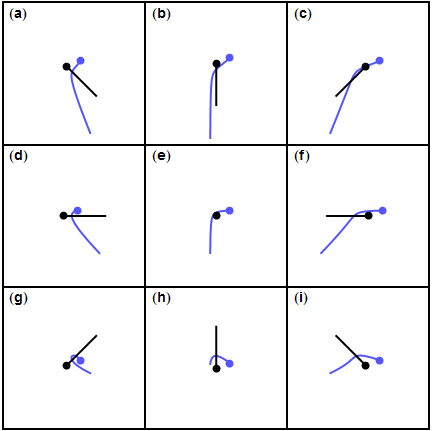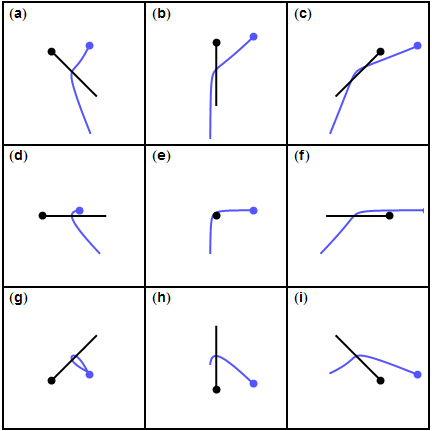
행성과 로켓의 상대적 운동의 여러 경우의 수를 보면 행성의 공전 방향과 로켓의 운동 방향이 서로 반대일 때, 로켓이 이전보다 빨라지는 걸 확인할 수 있습니다. 로켓은 소위 역주행을 할 때 추진력을 얻는 셈이죠.

 

역주행을 통해 추진력을 얻다.

 

10년 동안의 무명 생활로 그룹 해체 직전까지 갔지만 롤린의 기록적 역주행으로 2020년 대중의 원픽이 되었던 브레이브 걸스의 극적인 반전은 '시련과 고난은 언젠가는 극복될 수 있다.'는 역전 스토리로 승화되어 당시 코로나 19로 지쳐있는 많은 사람들에게 큰 위로와 용기가 되었습니다.

 

피는 시기가 다를 뿐, 피지 않는 꽃은 없다.

 

행성의 중력을 훔쳐 역주행 궤적을 그리며 미지의 곳을 향하는 로켓처럼, 대중의 마음을 훔쳐 성공의 궤적을 향해 역주행했던 브레이브 걸스의 '스윙 바이'는 삶은 멋진 긴 여정이고 성공에 너무 늦은 때란 없다는, 바래져 가던 진리에 다시 색을 입혀주었기에 사람들이 그토록 열광했던 게 아닐까요?

 

쏜살같이 흘러가버리는 하루처럼 인생 역시 너무나 짧으리라는 허망한 마음이 들면서도 그런 유한함이야말로 삶을 힘껏 살게 하는 구동력이라는 생각이 듭니다. 언젠가 피우게 될 여러분 각자의 꽃을 위해 그러한 구동력을 발판 삼아 '스윙 바이'하기를 응원합니다. 오늘도 물리를 통해 인생을 배웁니다.